LCA(Least Common Ancestor) - CyberFlower Algorithm

LCA 알고리즘이란 트리에서 2개의 노드가 주어졌을 때, 두 노드의 가장 가까운 공통조상을 찾는 알고리즘이다.

트리에서 어떤 노드 a의 조상이란 a에서 루트노드로 가는 최단경로상에 있는 모든 노드를 의미하며, 자기 자신(a)는 제외한다.

따라서 루트노드가 정의되어 있지 않는 트리 혹은 루트 노드가 정의되기 어려운 그래프에서는 LCA 알고리즘이 존재하지 않는다.

(즉, LCA 문제라면 1. 트리여야 하고, 2. 루트 노드가 있어야 한다.)

1. 탐색(전처리)을 제외하고 O(n)의 시간복잡도를 갖는 LCA

트리1

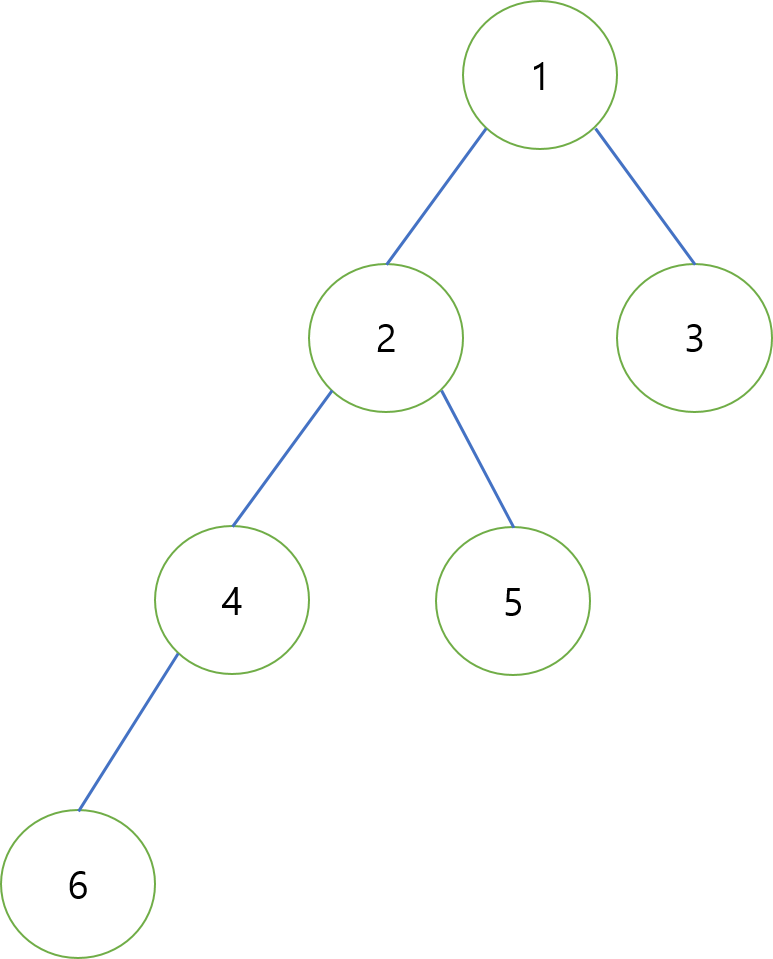
나이브하게 LCA를 찾는 방법으로는 두 노드에서 루트 노드를 향해 한 칸씩 올라가 보는 방법이 있다.

최악의 경우 루트노드까지의 거리는 n이므로 LCA를 한 번 구할때 마다 O(n)만큼의 시간복잡도가 필요하다.

알고리즘은 다음과 같다.

dfs(또는 다른 탐색 알고리즘)을 한 번 수행한다. 탐색 알고리즘을 한 번 수행하면서 노드의 정보를 update한다.

이때 update해야 하는 정보로는 해당 노드의 부모, 루트로부터의 거리(lv)이 있다. (전처리 과정으로, 복잡도는 O(n)이다.)

두 노드의 lv을 맞춰주자. 3번 노드와 6번 노드의 LCA를 찾는다고 한다면, 일단 3번 노드를 2번 노드까지 level_up을 시켜주어도 된다.

자명하게 3번 노드의 조상 중에서 2,4 노드는 공통조상이 될 수 없다.

lv이 같아졌다면, 이제는 두 노드가 만날때까지 한 칸씩 올라가면 된다. 3번 노드의 부모는 1, 6번 노드의 부모는 1이므로 LCA는 1이 된다.

const int SZ=100005; //maximum number of nodes, node is 1-n
vector<int> graph[SZ]; //tree
int par[SZ]; //parent, root's parent is 0
int lv[SZ]; //distance from root
int vst[SZ]; //check dfs
void dfs(int n, int parent, int level){
  vst[n]=1;
  lv[n]=level;
  par[n]=parent;
  for(int nxt:graph[n]){
    if(vst[nxt]==1) continue;
    dfs(nxt,n,level+1);
  }
}
int lca(int x, int y){
  if(lv[x]<lv[y]) swap(x,y);
  while(lv[x]>lv[y]){
    x=par[x];
  }
  while(x!=y){
    x=par[x];
    y=par[y];
  }
  return x;
}

2. 탐색을 제외하고 O(log(n))의 시간복잡도를 갖는 LCA

한 칸씩 차근차근 올라가는게 시간이 아깝다고 느낀다면 해당 방식을 써야만 한다. LCA를 한 번 찾는데 걸리는 시간은 O(log(n))이지만 전처리 과정의 복잡도는 O(nlog(n))임에 유의하자.

naive한 LCA 알고리즘에서는 부모를 일차원 배열에 저장했다면, 해당 알고리즘에서는 parse table이라고 불리는 2차원 memoization 배열에 조상을 저장한다.

parse_table[트리의 최대 높이][노드] 의 자료형을 갖고, parse_table[a][x]에는 x의 $2^x$번째 조상을 저장한다.

이렇게 하면 level_up을 O(1)으로 할 수 있게 되는데, 자세한 내용은 알고리즘 설명과 코드에서 보도록 하자.

알고리즘은 다음과 같다.

dfs 탐색을 한번 하여 각 노드들의 부모 노드와 lv을 update한다.

부모 노드는 $2^0$번째 조상이라고 할 수 있으므로 par[0][x]에 저장한다.

탐색을 한 번 진행했으므로 복잡도는 O(n)이다.

조상을 저장하는 parse table을 update한다.

par[a][x]=par[a-1][par[a-1][x]]라는 식이 성립한다. (x의 $2^a$번째 조상은 (x의 $2^{a-1}$) 조상의 $2^{a-1}$ 조상과 같다. )

1의 과정에서 par[0][x]를 구해놓았기 때문에, 우리는 n*(트리의 최대 높이)=nlog(n)의 복잡도로 parse table을 update할 수 있다.

두 노드의 lv을 맞춰주자. 만약 lv만 맞춰주었는데 두 노드가 같아졌다면, 해당 노드는 LCA이고 여기서 알고리즘을 끝낸다.

(대개의 경우 lv을 맞춰준다고 바로 LCA가 되지는 않는다. return을 잘 해주면 된다.)

두 노드의 공통조상을 찾는데, 이 방법이 naive 버전과 조금 다르다. 코드를 보자.

for(int i=MXH-1;i>=0;i--){
  if(par[i][x]!=par[i][y]){
    x=par[i][x];
    y=par[i][y];
  }
}
x=par[0][x];

트리2

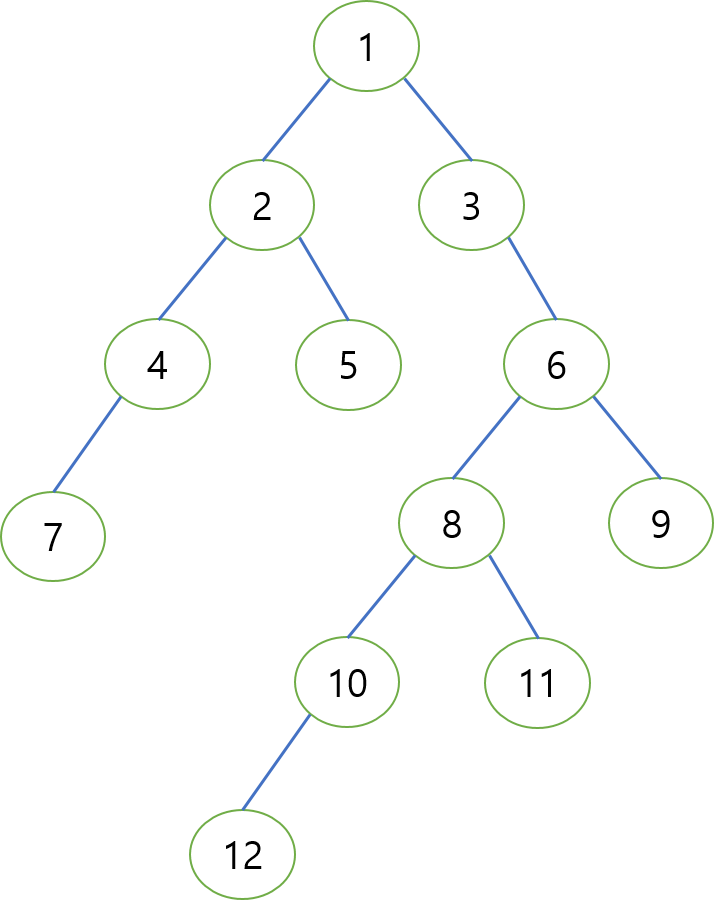
위 반복문에서 해주는 일은 LCA가 되기 직전 노드를 구해주는 일이다.

7과 12의 LCA를 구해보자. 일단은 12는 8로 level_up 되어 있는 상황일 것이다.

7과 8에서 $2^2$ 만큼 올라가면 0로 같아지므로 올라가지 않고, $2^1$ 만큼 올라가면 LCA

바로 직전 노드까지 올라가게 되어 x=2, y=3이 된다.

따라서 LCA는 x의 부모, 그리고 y의 부모인 1이 된다.

하지만 naive LCA에서 했던 것처럼 바로 LCA를 구하면 안 되는 걸까?

결론부터 말하자면 안된다. LCA(최소공통조상)가 아닌 CA(공통조상)로 jump할 수도 있고, 심지어는 루트인 1보다도 더 높은 노드 0(코딩의 편의를 위해 설정한 1의 부모) 로 뛰어버릴 수도 있기 때문이다.

알고리즘 설명이 끝났다. LCA 코드를 보자.

const int SZ=100005; //maximum number of nodes, node is 1-n
const int MXH=20; // max number of log_2(level)
vector<int> graph[SZ]; //tree
int lv[SZ]; //equal
int par[MXH][SZ]; //dp for parent
int vst[SZ]; //equal
int n; // number of nodes
void dfs(int x, int parent, int level){
  vst[x]=1;
  par[0][x]=parent;
  lv[x]=level;
  for(int nxt: graph[x]){
    if(vst[nxt]==1) continue;
    dfs(nxt,x,level+1);
  }
}
void memo(){
  for(int i=1;i<MXH;i++){
    for(int j=1;j<=n;j++){
      par[i][j]=par[i-1][par[i-1][j]];
    }
  }
}
int level_up(int x, int d){ // d is a number for lv up!
  for(int i=MXH-1;i>=0;i--){
    if(d&(1<<i)) x=par[i][x];
  }
  return x;
}
int query(int x, int y){
  x=level_up(x,max(0,lv[x]-lv[y])); // x와 y level 맞추기
  y=level_up(y,max(0,lv[y]-lv[x]));
  if(x==y) return x;
  for(int i=MXH-1;i>=0;i--){
    if(par[i][x]!=par[i][y]){
      x=par[i][x];
      y=par[i][y];
    }
  }
  x=par[0][x];
  return x;
}

LCA(Lowest Common Ancestor) 알고리즘

1. 탐색(전처리)을 제외하고 O(n)의 시간복잡도를 갖는 LCA

2. 탐색을 제외하고 O(log(n))의 시간복잡도를 갖는 LCA