백준 15480 LCA와 쿼리
https://www.acmicpc.net/problem/15480
쿼리마다 루트가 달라지지만, 루트를 1로 하는 트리를 통해 정답을 유추할 수 있습니다.
(루트가 달라질때마다 쿼리를 새로 구하기에는 노드의 숫자와 쿼리의 개수가 너무 많아요)
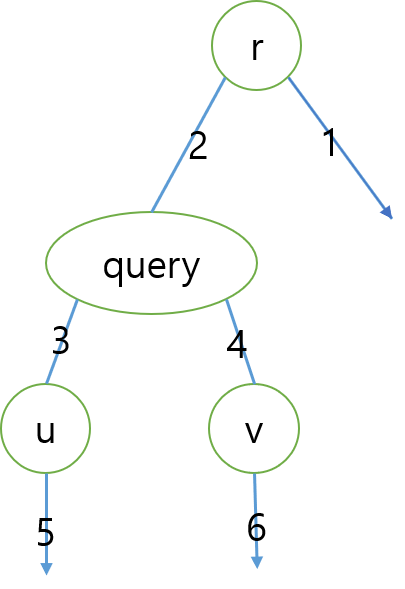
쿼리에서 나타난 루트를 기준으로 트리를 간단하게 나타내면 위의 그림처럼 나타낼 수 있습니다.
query라고 표시한 노드는 쿼리에서 주어진 루트와 두 노드에 대한 LCA를 나타냅니다.
그리고 1이 있을 수 있는 위치는 1,2,3,4,5,6 중에 하나입니다.
1: u, v가 포함되지 않는 sub tree에 1이 있는 경우
2: r과 q 사이에 1이 있는 경우
3: q와 u 사이에 1이 있는 경우
4: q와 v 사이에 1이 있는 경우
5: u의 subtree에 1이 있는 경우
6: v의 subtree에 1이 있는 경우
위 그래프에서 query를 구해봅시다. 1을 루트로 하는 트리와 연관성을 찾을 수 있을까요?
1: query=LCA(u,v), LCA(u,r)=r, LCA(v,r)=r
2: query=LCA(u,v), LCA(u,r)=1, LCA(v,r)=1
3:query=LCA(r,v), LCA(u,r)=1, LCA(u,v)=1
4:query=LCA(r,u), LCA(r,v)=1, LCA(u,v)=1
5:query=LCA(r,v), LCA(r,u)=u, LCA(u,v)=u
6:query=LCA(r,u), LCA(r,v)=v, LCA(u,v)=v
이제 규칙이 보이시나요? 다양한 규칙이 있겠지만, 제가 생각했을 때 가장 간단한 규칙은 1을 루트로 하는 트리에서 LCA(u,v), LCA(u,r), LCA(v,r) 중 level이 두번째로 큰 노드가 r을 루트로 하는 트리에서 u,v의 LCA입니다. (level: 루트에서부터의 거리)
이제 코드를 보죠.
#include<bits/stdc++.h>
using namespace std;
const int MXH = 18;
const int SZ = 100005;
typedef pair<int,int> pii;
vector<int> graph[SZ];
int lv[SZ];
int dp[MXH][SZ];
void dfs(int crt, int prt, int level){
lv[crt] = level;
dp[0][crt]=prt;
for(int next : graph[crt]){
if(next != prt){
dfs(next,crt,level+1);
}
}
}
int level_up(int n, int t){
for(int i=0;i<MXH;i++){
if((1<<i)&t) n=dp[i][n];
}
return n;
}
int LCA(int a, int b){
a = level_up(a,max(0,lv[a]-lv[b]));
b = level_up(b,max(0,lv[b]-lv[a]));
if(a==b) return a;
for(int i=MXH-1;i>=0;i--){
if(dp[i][a]!=dp[i][b]){
a = dp[i][a];
b = dp[i][b];
}
}
return dp[0][a];
}
int query(pii p1,pii p2,pii p3){
pii parr[3]={p1,p2,p3};
sort(parr,parr+3);
return parr[2].second;
}
int main(void){
ios::sync_with_stdio(false); cin.tie(NULL);
int n; cin>>n;
for(int i=1;i<n;i++){
int x,y; cin>>x>>y;
graph[x].push_back(y);
graph[y].push_back(x);
}
dfs(1,0,0);
for(int i=1;i<MXH;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i-1][dp[i-1][j]];
}
}
int m; cin>>m;
for(int i=0;i<m;i++){
int r,u,v; cin>>r>>u>>v;
int uv = LCA(u,v);
int ru = LCA(r,u); int rv = LCA(r,v);
cout<<query({lv[uv],uv},{lv[ru],ru},{lv[rv],rv})<<'\n';
}
return 0;
}
