백준 1626 두 번째로 작은 스패닝 트리
기본 아이디어는 다음과 같습니다.
- MST를 찾는다.
- MST에 포함되지 않는 간선들 중 하나를 추가해본다. 이 간선을 추가함으로써 지울 수 있는 가장 큰 간선을 하나 찾는다.
- 2의 과정을 반복하면서 추가하는 간선과 지우는 간선의 차이가 가장 작은 경우를 찾는다.
1번 과정은 prim 알고리즘을 사용하였습니다. 복잡도는 O(nlog(n))이므로 문제 없습니다. (전처리로 한번만 수행합니다.)
LCA를 사용할 수 있다는 아이디어를 떠올리면 2번을 쿼리당 log(n)으로 수행할 수 있음을 깨닫게 됩니다.
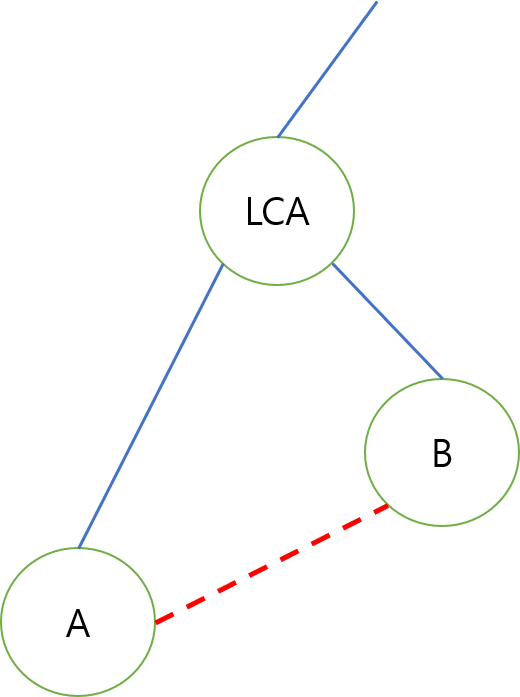
MST에 포함되지 않는 간선 AB를 추가하면 지울 수 있는 간선은 AB 경로상에 있는 간선 뿐입니다.
-
간선 하나를 추가하면 트리였던 MST에 A,B,LCA를 하는 삼각형(cycle)이 생깁니다. 이걸 다시 트리로 바꾸려면 지울 수 있는 간선은 AB 경로상에 있는 간선입니다.
-
AB 위에 있는 간선 중 어떤 간선을 지워도 괜찮습니다. 왜냐하면 AB가 연결되었으므로 트리의 성질 중 다른 간선과의 연결성을 만족하기 때문입니다.
이제 sparse table에 간선 가중치의 최댓값을 구하면 됩니다 라고 생각했지만…
최소 스패닝 트리보다는 크면서 가장 작은 스패닝 트리라는 조건이 있습니다.
추가하려는 간선과 지우려는 간선의 가중치가 같은 경우라면 처리하기 매우 까다롭겠네요.
따라서 두번째로 큰 가중치를 저장하는 sparse table을 하나 더 만들고, 경로에 두번째로 큰 가중치가 존재하지 않는다면 -1을 넣어줍니다. (경로상에 가중치들이 전부 동일하거나 경로에 간선이 하나인 경우 등등)
추가하려는 간선과 지우려는 간선의 가중치가 다른 경우라면 처음 아이디어대로 하면 됩니다.
같은 경우라면 이제 LCA jump를 하면서 두번째로 큰 가중치, 가장 큰 가중치들을 모두 모아줍니다. 여기서 두번째로 큰 가중치를 찾아야겠죠!
jump를 log(n)번 하고 jump당 2개의 후보가 생기기 때문에 나이브하게 모아서 정렬을 해 주어도
쿼리당 2log(n)log(2log(n)), 즉 log(n)log(log(n)) 만큼 시간이 더 걸리게 됩니다. 이정도는 괜찮겠네요.
3번 과정을 해야죠. m(그래프의 간선 개수)-n(트리의 간선 개수) 만큼 쿼리를 돌리면 됩니다. 최종 시간복잡도는 (m-n)log(n)log(log(n)) 이 됩니다.
#include<bits/stdc++.h>
#define ff first
#define ss second
using namespace std;
const int SZ=50005;
const int MXH=20;
vector<pair<int,int>> graph[SZ];
vector<pair<int,int>> tree[SZ];
int lv[SZ];
int par[MXH][SZ];
int dst[MXH][SZ]; // 가장 큰 가중치를 저장하는 sparse table
int dst_2[MXH][SZ]; // 두번째로 큰 가중치를 저장하는 sparse table
int prim_dst[SZ];
int vst[SZ];
int prim_vst[SZ];
int n;
void dfs(int x, int w, int parent, int level){
vst[x]=1;
par[0][x]=parent;
dst[0][x]=w;
lv[x]=level;
for(auto nxt: tree[x]){
if(vst[nxt.ff]==1) continue;
dfs(nxt.ff,nxt.ss,x,level+1);
}
}
bool myf(int x, int y){
return x>y;
}
int second_mx(vector<int> v){
sort(v.begin(),v.end(),myf);
auto it=unique(v.begin(),v.end());
v.resize(distance(v.begin(),it));
if(v.size()<=1) return v[0];
return v[1];
}
void memo(){
for(int i=1;i<MXH;i++){
for(int j=1;j<=n;j++){
par[i][j]=par[i-1][par[i-1][j]];
dst[i][j]=max(dst[i-1][j],dst[i-1][par[i-1][j]]);
dst_2[i][j]=second_mx({dst[i-1][j],dst[i-1][par[i-1][j]],dst_2[i-1][j],dst_2[i-1][par[i-1][j]]});
}
}
}
int level_up(int x, int d){
for(int i=MXH-1;i>=0;i--){
if(d&(1<<i)) x=par[i][x];
}
return x;
}
int lca(int x, int y){
x=level_up(x,max(0,lv[x]-lv[y]));
y=level_up(y,max(0,lv[y]-lv[x]));
if(x==y) return x;
for(int i=MXH-1;i>=0;i--){
if(par[i][x]!=par[i][y]){
x=par[i][x];
y=par[i][y];
}
}
x=par[0][x];
return x;
}
int max_dist(int x, int y, int u, int w){
int ans=0;
vector<int> tmp;
int dx=lv[x]-lv[u];
int dy=lv[y]-lv[u];
for(int i=MXH-1;i>=0;i--){
if(dx&(1<<i)){
ans=max(ans,dst[i][x]);
tmp.push_back(dst[i][x]);
tmp.push_back(dst_2[i][x]);
x=par[i][x];
}
}
for(int i=MXH-1;i>=0;i--){
if(dy&(1<<i)){
ans=max(ans,dst[i][y]);
tmp.push_back(dst[i][y]);
tmp.push_back(dst_2[i][y]);
y=par[i][y];
}
}
if(ans!=w) return ans;
return second_mx(tmp);
}
int prim(){
int ans=0;
for(int i=1;i<=n;i++) prim_dst[i]=INT_MAX;
priority_queue<pair<int,pair<int,int>>> pq;
prim_dst[1]=0;
pq.push({-prim_dst[1],{1,0}});
while(!pq.empty()){
auto t=pq.top(); pq.pop();
if(prim_dst[t.ss.ff]!=-t.ff) continue;
prim_vst[t.ss.ff]=1;
tree[t.ss.ff].push_back({t.ss.ss,-t.ff});
tree[t.ss.ss].push_back({t.ss.ff,-t.ff});
for(auto nxt: graph[t.ss.ff]){
if(prim_vst[nxt.ff]==1) continue;
if(prim_dst[nxt.ff]>nxt.ss){
prim_dst[nxt.ff]=nxt.ss;
pq.push({-prim_dst[nxt.ff],{nxt.ff,t.ss.ff}});
}
}
}
for(int i=1;i<=n;i++){
if(prim_dst[i]==INT_MAX) return -1;
ans+=prim_dst[i];
}
return ans;
}
int main(void){
ios::sync_with_stdio(false); cin.tie(NULL);
memset(dst_2,-1,sizeof(dst_2));
int m; cin>>n>>m;
for(int i=0;i<m;i++){
int x,y,z; cin>>x>>y>>z;
graph[x].push_back({y,z});
graph[y].push_back({x,z});
}
int tot=prim();
if(tot==-1){
cout<<-1;
return 0;
}
dfs(1,0,0,0);
memo();
int ans=INT_MAX;
for(int i=1;i<=n;i++){
for(auto x:graph[i]){
if(par[0][i]==x.ff || par[0][x.ff]==i) continue;
int md=max_dist(i,x.ff,lca(i,x.ff),x.ss);
if(md==-1) continue;
ans=min(ans,x.ss-md);
}
}
if(ans==INT_MAX){
cout<<-1;
return 0;
}
cout<<tot+ans;
return 0;
}
