icpc.me 17402

https://www.acmicpc.net/problem/17402

N*M 크기의 게임판에서 행과 열을 최대한 선택하는데, 선택한 행과 열의 교차점에 X가 존재하지 않도록 최대한 많이 선택하는 문제입니다. 간단한 플로우 문제이지만 konig’s theorem과 같은 관련 지식을 알아야 쉽게 해결방법을 찾을 수 있습니다.

문제를 다음과 같이 바꿀 수 있습니다. i번째 행 j번째 열의 점에 X표시가 되어있다면, 왼쪽에서 i번째 정점과 오른쪽에서 j번째 정점이 간선으로 연결시키도록 하여 그래프를 그릴 수 있습니다. 문제의 예시를 바꾸면 다음 그림과 같습니다.

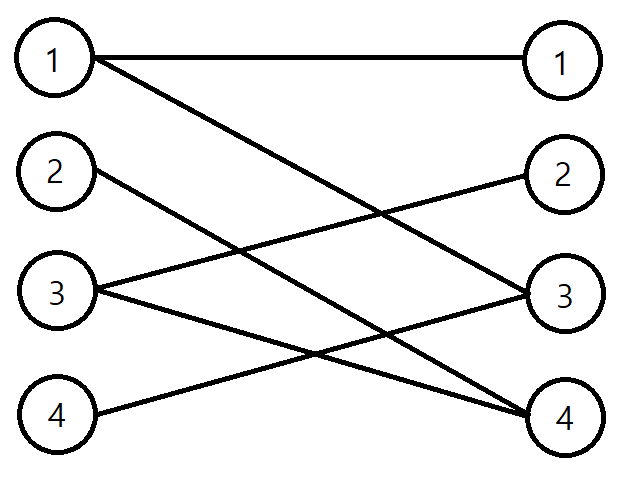
그렇다면 이 그래프에서 어떤 두 정점도 간선으로 연결되지 않게 정점을 최대한 많이 선택하는 것이 문제의 해답이 됨을 알 수 있습니다. 이는 konig’s theorem으로 해결할 수 있습니다.

konig’s theorem을 설명하기 앞서 maximum independent set과 minimum vertex cover, maximum matching에 대하여 알아야 합니다.

independent set이란 그래프에서 어떤 두 정점도 간선으로 연결되지 않은 정점의 집합이며 maximum independet set이란 independent set중 정점의 개수가 가장 큰 집합입니다.

vertex cover란 그래프에서 모든 간선이 적어도 어떤 한 정점과 연결되어 있는 정점의 집합이며 minimum vertex cover란 vertex cover중 정점의 개수가 가장 작은 집합입니다.

maximum independent set에 속한 정점의 개수와 minimum vertex cover에 속한 정점의 개수를 더하면 그래프의 모든 정점의 개수가 됩니다.

matching이란 그래프에서 어떤 두 간선도 같은 정점을 공유하지 않는 간선의 집합이며 maximum matching이란 matching중 간선의 개수가 가장 많은 집합입니다.

konig’s theorem이란 이분 그래프에서 minimum vertex cover의 크기와 maximum matching의 크기가 같다는 정리입니다. 우리의 목표는 어떤 두 정점도 간선으로 연결되지 않게 정점을 최대한 많이 선택하는 것으로 maximum indepedent set의 크기를 구하는 것과 같고, 전체 정점의 개수에서 minimum vertex cover에 속한 정점의 개수를 빼서 구할 수 있습니다. konig’s thoerem에 따라 minimum vertex cover의 크기와 maximum maching의 크기가 같으므로 이분 매칭 알고리즘을 통해 maximum matching을 구하여 전체 정점의 개수에서 빼주면 정답을 구할 수 있습니다.

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int MAXV=205;
int n,m,k,A[MAXV],B[MAXV],vst[MAXV];
vector<int> adj[MAXV];
int dfs(int a)
{
	vst[a]=1;
	for(auto b:adj[a])
	{
		if(B[b]==-1||(!vst[B[b]]&&dfs(B[b])))
		{
			A[a]=b;
			B[b]=a;
			return 1;
		}
	}
	return 0;
}
int main(void)
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cin>>n>>m>>k;
	for(int i=1;i<=k;i++)
	{
		int x,y; cin>>x>>y;
		adj[x].pb(y);
	}
	fill(A,A+MAXV,-1);
	fill(B,B+MAXV,-1);
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		if(A[i]==-1)
		{
			fill(vst,vst+MAXV,0);
			if(dfs(i)) ans++;
		}
	}
	cout<<(n+m-ans);
	return 0;
}