icpc.me 3830 - CyberFlower Algorithm

https://www.acmicpc.net/problem/3830

union-find + online/offline query를 이용하여 해결했습니다. 쿼리를 모두 받아서 그래프를 다 완성하고 질의를 하는 것과 쿼리를 받는 중간에 질의를 하는 것의 차이는 UNKNOWN이냐 아니냐의 차이 뿐입니다. UNKNOWN이 아니라면 값은 동일합니다.

따라서 ?가 입력이 되면 현재 두 노드가 연결이 되어 있는지 union-find를 통해 O(1)의 시간복잡도로 알 수 있고, 연결되어 있지 않는다면 미리 UNKNOWN을 저장해둡니다.

쿼리를 다 받은 후 offline에서 완성된 그래프에 대하여 무게 차이를 구합니다. (UNKNOWN이 아니라면 그래프가 완성된 후에 무게 차이를 구해도 답은 동일합니다.)

무게는 각 그룹에서 가장 가벼운 물건을 기준으로 얼마나 더 무거운지를 탐색과정에서 배열에 저장하였습니다. (union-find에서 그룹의 대표값이 가장 가벼운 물건이 되도록 설정할 수 있습니다.)

#include<bits/stdc++.h>
#define ff first
#define ss second
#define pb push_back
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int SZ=100005;
const int MXJ=20;
vector<pii> graph[SZ];
int uni[SZ];
int vst[SZ];
ll dst[SZ];
pii qry[SZ];
int n,m;
int find(int x){
	if(x==uni[x]) return x;
	return uni[x]=find(uni[x]);
}
void merge(int x, int y){
	x=find(x);
	y=find(y);
	uni[y]=x;
}
void dfs(int x, ll d){
	vst[x]=1;
	dst[x]=d;
	for(pii nxt:graph[x]){
		if(vst[nxt.ff]==1) continue;
		dfs(nxt.ff,d+(ll)nxt.ss);
	}
}
void memo(){
	for(int i=1;i<=n;i++){
		if(vst[i]==0) dfs(find(i),0);
	}
}
void init(){
	for(int i=1;i<=n;i++){
		uni[i]=i;
		graph[i].clear();
	}
	memset(dst,0,sizeof(dst));
	memset(vst,0,sizeof(vst));
}
int main(void){
	ios::sync_with_stdio(false); cin.tie(NULL);
	while(1){
		cin>>n>>m;
		if(n==0 && m==0) break;
		init();
		int p=0;
		for(int i=0;i<m;i++){
			char o; cin>>o;
			if(o=='!'){
				int x,y,z; cin>>x>>y>>z;
				merge(x,y);
				graph[x].pb({y,z});
				graph[y].pb({x,-z});
			}
			else if(o=='?'){
				int x,y; cin>>x>>y;
				if(find(x)!=find(y)) qry[p++]={-1,-1};
				else qry[p++]={x,y};
			}
		}
		memo();
		for(int i=0;i<p;i++){
			if(qry[i].ff==-1) cout<<"UNKNOWN"<<'\n';
			else cout<<dst[qry[i].ss]-dst[qry[i].ff]<<'\n';
		}
	}
	return 0;
}

사실 union-find로만 짤 수 있는 방법이 있습니다! 다음 방법에서도 dist 배열에는 subtree에서 가장 작은 가중치와의 차이를 저장합니다.

union-find는 sub-tree 2개를 1개로 합치는 과정이라 볼 수 있습니다. 따라서 merge 과정에서는 root가 되지 못하는 sub-tree의 루트의 dist를 update하고, find 과정에서 이를 반영해 줍니다.

find 과정

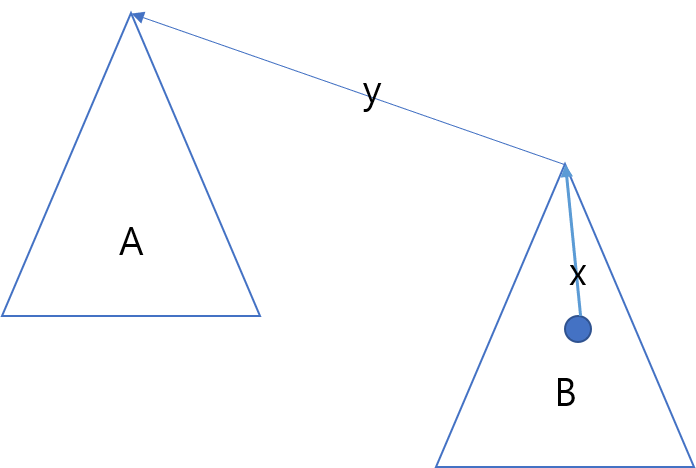
union-find

B의 subtree 안에 있는 노드 n은 merge 후에도 x가 저장이 되어 있을 겁니다. 하지만 우리는 x+y를 찾아야 하죠. 따라서 find 과정에서 업데이트 되기 전 루트노드에 저장되어 있는 dist값인 y를 더해주면 됩니다.

merge 과정

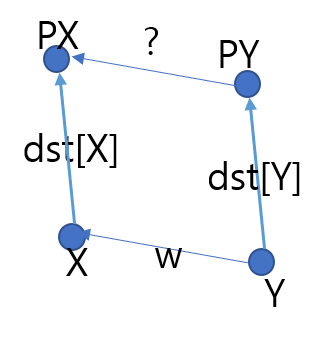
union-find

하지만 find를 제대로 수행하기 위해서는 연결되기 전 subtree의 루트였던 값들이 merge에서 제대로 update가 되어야 합니다. 어떻게 하면 될까요?

서로 다른 두 집합에 있던 X,Y를 연결하는 상황을 생각해봅시다. (같은 집합에 있었다면 merge하지 않아도 됩니다.) PX는 연결되기 전 X가 속해있는 집합의 대표값이고, PY는 Y가 속해있는 집합의 대표값입니다.

연결되기 전 dst[PX], dst[PY]는 0이 될겁니다. 우리는 merge에서 PX, PY 중에서 누가 루트가 될 지 고르고 루트가 아닌 노드의 dst를 update해야 합니다.

dst[PY] 를 update한다고 가정합시다. dst[PY]=dst[X]+w-dst[Y]라는 식이 성립할 겁니다.(그림을 참고해 주세요!) dst[X]+w-dst[Y]>0 이라면 PX의 무게가 가장 작기 때문에 dst[PY]를 update해준 뒤 PY의 부모를 PX로 update해주면 됩니다.

0보다 작다면 PY가 루트가 되겠네요. 반대로 해줍시다.

두번째 방법의 코드를 봅시다!

#include<bits/stdc++.h>
using namespace std;
const int SZ=100005;
typedef long long ll;
ll dst[SZ];
int par[SZ];
int find(int x){
	if(x==par[x]) return x;
	int px=find(par[x]);
	dst[x]+=dst[par[x]];
	return par[x]=px;
}
void merge(int x, int y, ll w){
	int px=find(x);
	int py=find(y);
	if(px==py) return;
	ll nd=dst[x]+w-dst[y];
	if(nd>0){
		par[py]=px;
		dst[py]=nd;
	}
	else{
		par[px]=py;
		dst[px]=-nd;
	}
}
int main(void){
	ios::sync_with_stdio(false); cin.tie(NULL);
	while(1){
		int n,m; cin>>n>>m;
		if(n==0 && m==0) break;
		for(int i=1;i<=n;i++){
			par[i]=i;
			dst[i]=0LL;
		}
		for(int i=0;i<m;i++){
			char op; cin>>op;
			if(op=='!'){
				int x,y,z; cin>>x>>y>>z;
				merge(x,y,z);
			}
			else if(op=='?'){
				int x,y; cin>>x>>y;
				if(find(x)!=find(y)) cout<<"UNKNOWN"<<'\n';
				else{
					cout<<dst[y]-dst[x]<<'\n';
				}
			}			
		}
	}
	return 0;
}

백준 3830 교수님은 기다리지 않는다

find 과정

merge 과정