볼록 껍질, 로버트 후드
1. 볼록 껍질(Convex Hull) 알고리즘
Convex Hull 알고리즘은 기하를 대표하는 알고리즘 중 하나이다. Convex Hull이란, 좌표들 중 일부를 선으로 연결하여 모든 점을 내부에 포함하게 하는 볼록다각형을 의미한다.
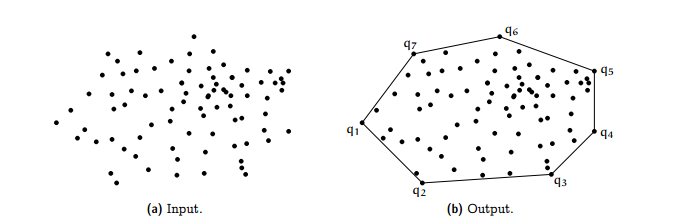
https://medium.com 에서 가져온 볼록껍질 이미지이다. 그림을 보는 게 이해가 더 쉬울 듯 하여 가져왔지만, 문제가 될 시 삭제하도록 하겠다.
Convex Hull 알고리즘의 개관은 다음과 같다.
- x 좌표가 가장 왼쪽에 있는 좌표 하나를 찾는다. 그러한 점이 여러개라면 가장 y 과표가 작은 점을 기준으로 한다.
- 각도에 따라 좌표를 정렬한다. 반시계 방향으로 정렬되도록 ccw를 활용하면 된다. 이 때, 1에서 찾았던 좌표 하나는 정렬하지 않음 과 각도가 같은 점이 여러개인 경우 첫번째 원소와 더 가까운 점을 기준으로 정렬 함 에 유의하여라.
- 정렬한 좌표를 바탕으로 첫번째 좌표부터 최근 두 원소와 새로운 원소가 ccw(반시계 방향)을 이룬다면 좌표를 볼록껍질(스택)에 추가해 나간다. 아니라면 ccw를 이룰때까지 스택의 위에 있는 원소를 뽑고 3개의 원소가 ccw인지 확인한다.
- 스택에 있는 원소가 볼록 껍질(Convex Hull)에 포함되는 원소들이다.
모든 좌표에 대하여 스택에 들어가거나 나오는 횟수가 최대 2회 이므로 볼록껍질을 완성하는 시간 복잡도는 O(N)이 된다. 정렬하는 시간복잡도가 O(NlogN)이므로 볼록껍질을 찾는 시간복잡도는 O(NlogN)이 된다.
1,2,4 까지는 감각적으로 이해가 되지만, 3번의 경우는 조금 아리송하다. 그림을 통해 알아보자.
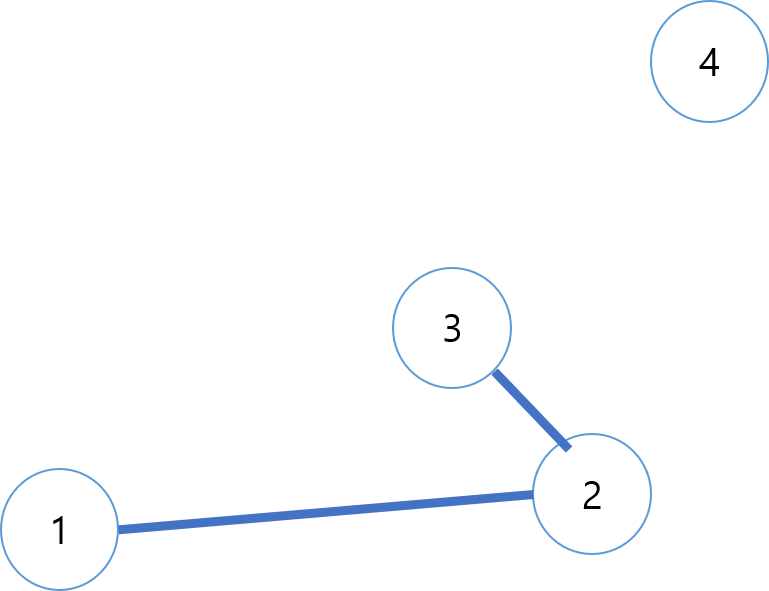
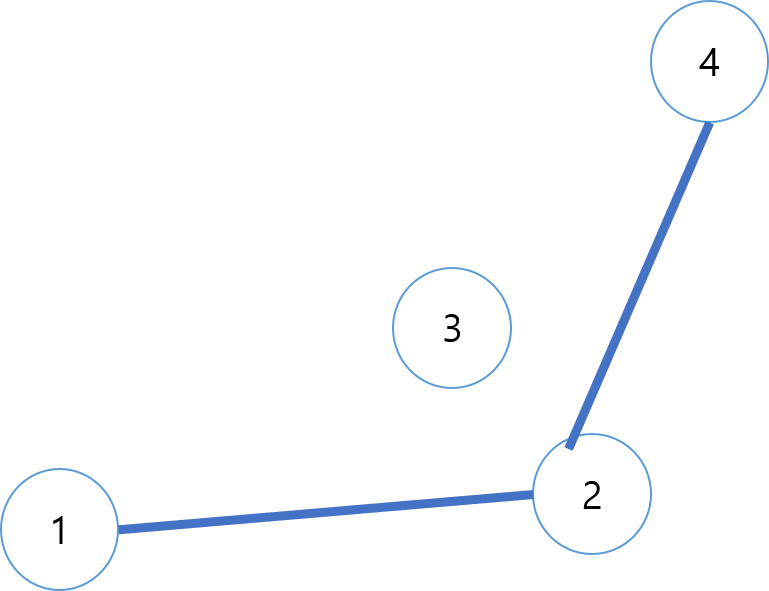
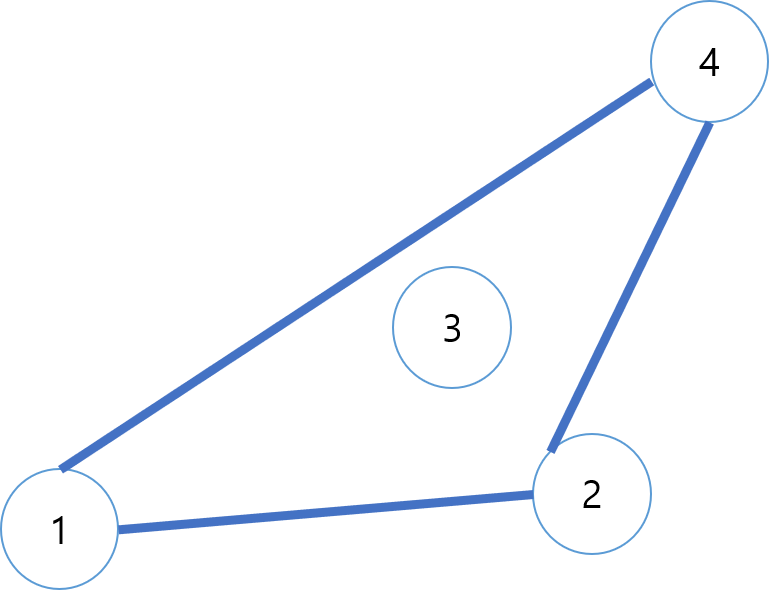
스택에 추가하는 과정에서 ccw가 -1(시계 방향)인 점이 생긴다면 스택의 top에 있는 점을 포함하는 볼록 다각형을 만들 수 있다. 3번 점을 보자. 4번 점이 추가되면 2,3,4에서 ccw가 음수가 나오게 된다. 간선 2,4가 3번 외부에 있기 때문이다. 따라서 우리는 stack의 top에 있던 3을 뽑아야 한다.
결과론적으로 연속하는 3개의 원소의 ccw가 모두 1이므로 최종적인 다각형이 볼록 다각형임을 다시 한 번 확인할 수 있다.
코드는 문제 이름부터 볼록 껍질인 https://www.acmicpc.net/problem/1708 의 코드를 보자.
#include<bits/stdc++.h>
#define x first
#define y second
#define pb push_back
using namespace std;
const int SZ=100005;
typedef long long ll;
typedef pair<ll,ll> pii;
pii pnt[SZ];
int ccw(pii a, pii b, pii c){
ll chk=a.x*b.y+b.x*c.y+c.x*a.y-(a.y*b.x+b.y*c.x+c.y*a.x);
return chk!=0LL?(chk>0?1:-1):0;
}
bool cmp(pii a, pii b){
int chk=ccw(pnt[0],a,b);
if(chk!=0) return chk>0? true:false;
if(a.x==b.x) return a.y<b.y;
return a.x<b.x;
}
int main(void){
ios::sync_with_stdio(false); cin.tie(NULL);
int n; cin>>n;
cin>>pnt[0].x>>pnt[0].y;
for(int i=1;i<n;i++){
cin>>pnt[i].x>>pnt[i].y;
if(pnt[0]>pnt[i]) swap(pnt[0],pnt[i]);
}
sort(pnt+1,pnt+n,cmp);
vector<int> st;
st.pb(0); st.pb(1);
int idx=2;
while(idx<n){
while(st.size()>=2 && ccw(pnt[st[st.size()-2]],pnt[st[st.size()-1]],pnt[idx])<=0){
st.pop_back();
}
st.pb(idx++);
}
cout<<st.size();
return 0;
}
2. Rotating Calipers를 이용하여 가장 먼 두 점 구하기
Rotating Calipers란 말 그대로 캘리퍼스를 돌려가면서 문제를 풀겠다는 뜻이다. 가장 먼 두 점을 구할때는 볼록 다각형을 캘리퍼스에 대강 끼워넣고, 캘리퍼스에서 볼록다각형을 돌려가면서 최대 거리를 구한다. (캘리퍼스는 2개의 평행한 선으로 이루어져 선분의 간격 차이로 물체의 길이를 측정하는 도구로써, 두 선분이 자유롭게 벌어진다.)
우리는 손쉽게 x좌표가 가장 작은 점과 가장 큰 점을 기준으로 캘리퍼스에 볼록다각형을 끼울 수 있다.
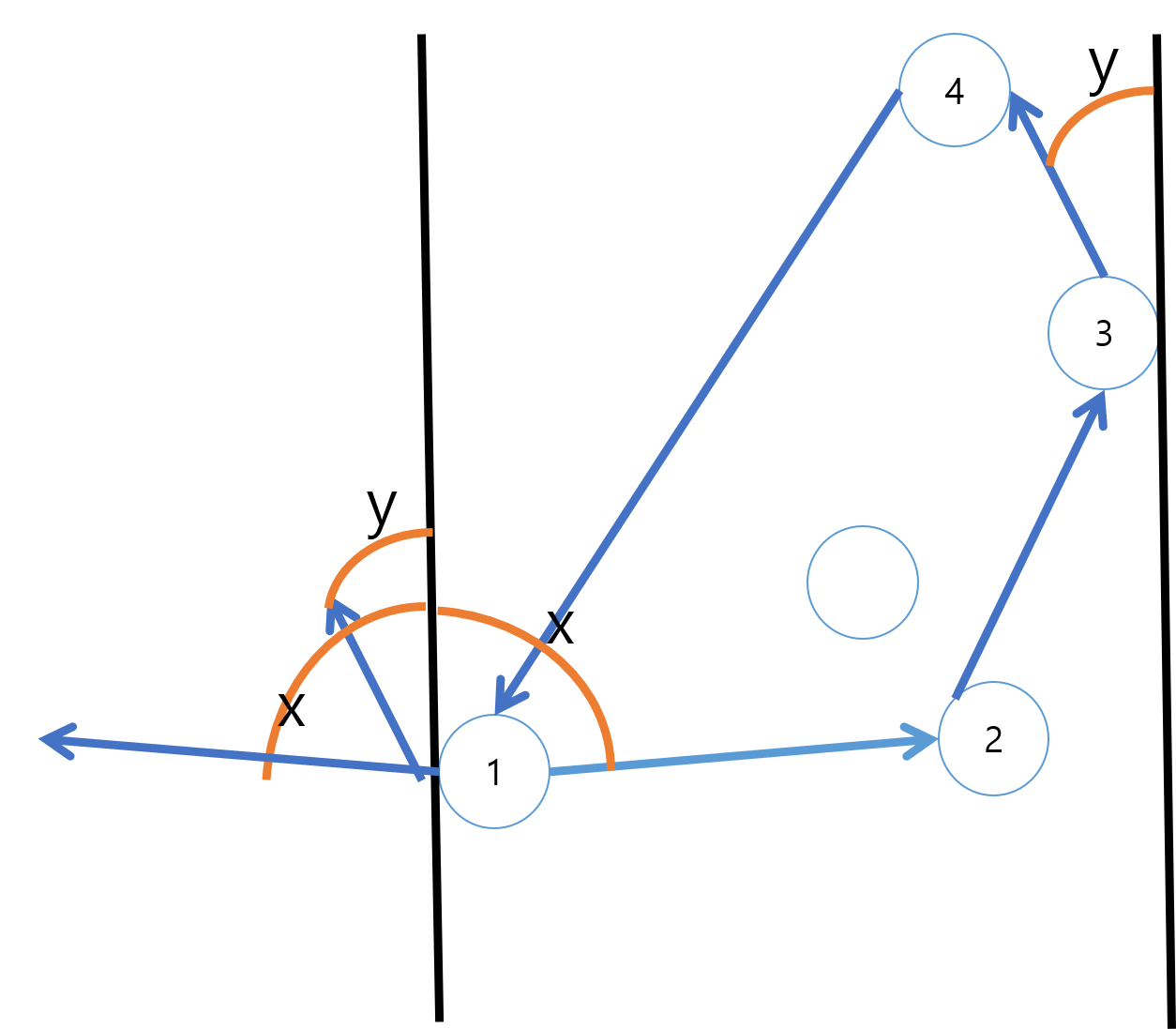
평행한 두 선분과 (1,2) (3,4) 가 이루는 각을 비교하는 방법 중 하나는 벡터의 외적을 이용하는 방법이다. (각도를 구해도 되지만, 실수 오차가 생길 수 있다.) 두 벡터가 한 점에서 만날 수 있도록 평행이동 한 후, 그림 처럼 벡터 하나를 $ 2\times PI-\theta $ 만큼 돌려주면 각을 비교할 수 있다. 이때, $ 2\times PI-\theta $ 회전한 벡터가 하나 있으므로 외적에 -1이 곱해짐에 유의하라.
즉, 벡터 2개를 원점에서(코딩의 편의상) 만날 수 있도록 평행이동 해준 후, ccw를 구했을 때 그림처럼 반시계 방향(-1을 곱해야 하므로 ccw<0)인 상황에서는 x가 더 크므로 3에서 회전하고, ccw>0인 상황에서는 1에서 회전해준다.
Rotating Calipers의 시간복잡도가 O(n)이라 가장 먼 두점을 구하는데 필요한 복잡도는 Convex Hull을 구하는 복잡도인 O(nlog(n))이 된다.
https://www.acmicpc.net/problem/9240 로버트 후드 문제의 코드이다.
#include<bits/stdc++.h>
#define x first
#define y second
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const int SZ=100005;
vector<pll> st;
pll pnt[SZ];
int ccw(pll a, pll b, pll c){
ll chk=a.x*b.y+b.x*c.y+c.x*a.y-(a.y*b.x+b.y*c.x+c.y*a.x);
return chk!=0LL?(chk>0LL?1:-1):0;
}
bool cmp(pll a, pll b){
int chk=ccw(pnt[0],a,b);
if(chk!=0) return chk>0?true:false;
return a.x==b.x?a.y<b.y:a.x<b.x;
}
ll dst(pll a, pll b){
return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
pll dif(int idx){
pll nxt=st[(idx+1)%st.size()];
return {st[idx].x-nxt.x,st[idx].y-nxt.y};
}
int main(void){
ios::sync_with_stdio(false); cin.tie(NULL);
int n; cin>>n;
cin>>pnt[0].x>>pnt[0].y;
for(int i=1;i<n;i++){
cin>>pnt[i].x>>pnt[i].y;
if(pnt[0]>pnt[i]) swap(pnt[0],pnt[i]);
}
sort(pnt+1,pnt+n,cmp);
st.pb(pnt[0]); st.pb(pnt[1]);
int idx=2;
while(idx<n){
while(st.size()>=2 && ccw(st[st.size()-2],st[st.size()-1],pnt[idx])<=0){
st.pop_back();
}
st.pb(pnt[idx++]);
}
int p1=min_element(st.begin(),st.end())-st.begin();
int p2=max_element(st.begin(),st.end())-st.begin();
ll ans=dst(st[p1],st[p2]);
int sz=st.size();
for(int i=0;i<n;i++){ // 각도가 작은 쪽으로 회전
if(ccw(dif(p1),{0,0},dif(p2))>0) p1=(p1+1)%sz; // 반시계 p1 증가
else p2=(p2+1)%sz;
ans=max(ans,dst(st[p1],st[p2]));
}
cout.precision(15);
cout<<sqrt(ans);
return 0;
}
