MCMF(Minimum Cost Maximum Flow)
1. MCMF 알고리즘이란?
Dinic이 Network Flow 알고리즘의 첫번째 꽃이였다면 MCMF 알고리즘은 Network Flow 알고리즘의 마지막 꽃이라고 할 수 있습니다. 그렇다면 MCMF가 무엇일까요? 일단 MCMF는 Minimum Cost Maximum Flow의 약자입니다. 한글로 풀어서 설명하자면, 가장 많은 유량을 보낼 수 있는 경우 중에서 비용이 가장 싼 것을 찾는 문제에요.
Source에서 Synk로 물을 흘린다고 가정합시다. 다른 플로우 문제와 마찬가지로 Source와 Synk 사이에는 여러개의 노드와 간선이 있습니다. 하지만 간선에 물을 흘리기 위해서는 우리는 돈을 지불해야 합니다.
F.F와 E.K를 공부할때 역간선(잔여용량)에 대해 공부했던 것이 기억나시나요? 우리는 통행료에 대해서도 역간선을 고려해줄 필요가 있습니다. 물을 흘려야 하나? 라고 생각해서 돈을 냈는데 만약 물을 흘리지 않는 것이 최선이라면 돈을 돌려줘야 되기 때문이죠. 따라서 우리는 역간선에 -c(c는 간선의 통행료)에 해당하는 통행료를 매길 필요가 있습니다.
(잔여용량의 경우 처음에는 (capacity,0)으로 설정되어 있다가 f의 flow가 흐르면 (capacity-f,f)로 바뀝니다. 하지만 통행료의 경우에는 늘어나거나 줄어들 필요가 없이 (fee,-fee)로 일정함에 유의합시다.)
MCMF 알고리즘의 개관에 대하여 설명하겠습니다.
- 가장 싸게 Synk로 도착할 수 있는 최단경로를 찾습니다.
- 1에서 찾은 최단경로로 물을 흘려보냅니다.
- Synk로 물이 가지 못할때 까지 1,2를 반복합니다.
1번 과정에서 최단경로를 찾는 알고리즘은 무엇이 있을까요? 다익스트라? 벨만 포드? 일단 다익스트라는 땡입니다. 음의 통행료가 있기 때문이죠. 그렇다고 벨만 포드를 쓰기에는 너무 느립니다. 이제 SPFA(Shortest Path Fastest Algorithm)을 배울 차례입니다.
2. SPFA 알고리즘 (Shortest Path Fastest Algorithm)
벨만포드의 성능을 향상시킨 알고리즘입니다. 음수 사이클이 존재할 경우(최악의 경우) 시간복잡도는 O(VE)로 벨만포드와 동일하지만 음수 사이클이 존재하지 않는 경우 시간복잡도가 O(V+E)가 되어 시간복잡도가 좋아집니다.
후에 설명할 MCMF에서 SPFA 알고리즘을 사용하게 되는데, MCMF알고리즘에서 음수 간선은 존재하지만 음수 사이클은 존재하지 않기 때문입니다. 간단한 증명을 보고 가겠습니다.
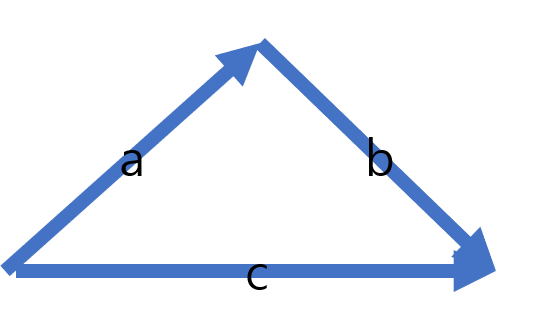
a+b>c 라고 해봅시다. c가 최단경로이기 때문에 c로 물이 흐르고, -c의 역간선이 생기게 됩니다. 하지만 a+b-c>0이기 때문에 사이클은 여전히 음수가 아닙니다.
이제 SPFA 알고리즘의 개관을 보도록 하겠습니다.
- dist 배열을 INF(무한대)로 초기화합니다.
- 시작 노드의 거리를 0으로 한 후 큐에 넣어줍니다.
- 큐의 첫번째 원소와 인접한 모든 노드들에 대하여 거리를 비교합니다. 3-1. 만약 거리가 줄어들었다면, 인접한 노드를 큐에 넣고 거리를 업데이트 해줍니다. 3-2. 큐에 들어있지 않은 원소가 update되었다면 큐에 넣어줍니다. 3-3. 현재 사용한 최단경로를 나중에 추적할 수 있도록 부모 노드에 대한 정보도 업데이트 해줍니다.
3. MCMF 알고리즘
MCMF 알고리즘 개관을 보도록 하겠습니다.
- SPFA 알고리즘을 돌립니다. synk까지 가는 경로가 존재한다면,
- 1에서 찾은 경로를 재탐색하면서 flow를 흘리고 비용을 구합니다.
- 현재까지 필요한 총 액수를 누적시킵니다.
- 1에서 synk까지 가는 경로가 존재하지 않을때까지 1,2,3을 반복합니다.
대표적인 MCMF 문제인 열혈강호5 문제입니다.
#include<bits/stdc++.h>
#define INF (int)1e9
#define pb push_back
#define ff first
#define ss second
using namespace std;
typedef pair<int,int> pii;
struct MCMF{
struct Edge{
int to,rev,cap,cost;
Edge(int to, int rev, int cap, int cost):to(to),rev(rev),cap(cap),cost(cost){
}
};
vector<vector<Edge>> graph;
vector<pii> par;
int n,src,snk;
MCMF(int n, int src, int snk):n(n),src(src),snk(snk){
graph.resize(n+5);
par.resize(n+5);
}
void push_edge(int a, int b, int capa, int cst){
graph[a].pb(Edge(b,graph[b].size(),capa,cst));
graph[b].pb(Edge(a,graph[a].size()-1,0,-cst));
}
bool SPFA(){
vector<int> inq,dst;
inq.resize(n+5,0);
dst.resize(n+5,INF);
queue<int> q;
q.push(src); inq[src]=1; dst[src]=0;
while(!q.empty()){
int h=q.front(); q.pop();
inq[h]=0;
for(int i=0;i<(int)graph[h].size();i++){
auto e=graph[h][i];
if(e.cap<=0) continue;
if(dst[h]<INF && dst[e.to]>dst[h]+e.cost){
dst[e.to]=dst[h]+e.cost; par[e.to]={h,i};
if(inq[e.to]==0){
q.push(e.to);
inq[e.to]=1;
}
}
}
}
return dst[snk]!=INF;
}
pii flow(){
int work=0,money=0;
while(SPFA()){
int c=0, f=INF;
for(int i=snk;i!=src;i=par[i].ff){
auto &e=graph[par[i].ff][par[i].ss];
f=min(f,e.cap);
c+=e.cost;
}
work+=f;
money+=f*c;
for(int i=snk;i!=src;i=par[i].ff){
auto &e=graph[par[i].ff][par[i].ss];
e.cap-=f;
graph[e.to][e.rev].cap+=f;
}
}
return {work,money};
}
};
int main(void){
ios_base::sync_with_stdio(false); cin.tie(NULL);
int n,m; cin>>n>>m;
MCMF mc=MCMF(n+m,0,n+m+1);
for(int i=1;i<=n;i++) mc.push_edge(mc.src,i,1,0);
for(int i=1;i<=n;i++){
int x; cin>>x;
for(int j=0;j<x;j++){
int y,c; cin>>y>>c;
mc.push_edge(i,y+n,1,c);
}
}
for(int i=n+1;i<=n+m;i++) mc.push_edge(i,mc.snk,1,0);
pii ans=mc.flow();
cout<<ans.ff<<'\n'<<ans.ss;
return 0;
}
