icpc.me 17428

https://www.acmicpc.net/problem/17428

괄호 문자열이란 빈 문자열과, 괄호 문자열 S와 T에 대해서 (S)와 ST의 두 규칙으로 만들어지는 문자열입니다. ‘(‘가 ‘)’보다 사전순으로 앞설 때, k번째 괄호 문자열을 찾는 문제입니다.

먼저 괄호 문자열은 정상적으로 열고 닫히는 문자열입니다. 즉, ‘(‘에 맞는 짝 ‘)’가 유일하게 존재하는 문자열입니다. (), (()), (()()) 등은 괄호 문자열이지만, ),())(, )()() 등은 괄호 문자열이 아닙니다.

일단 이러한 문자열의 개수를 구하는 방법은 이미 잘 알려져 있습니다. 카탈란 수라 불리는데, 이와 관련지어 생각하여 풀 수 있습니다.

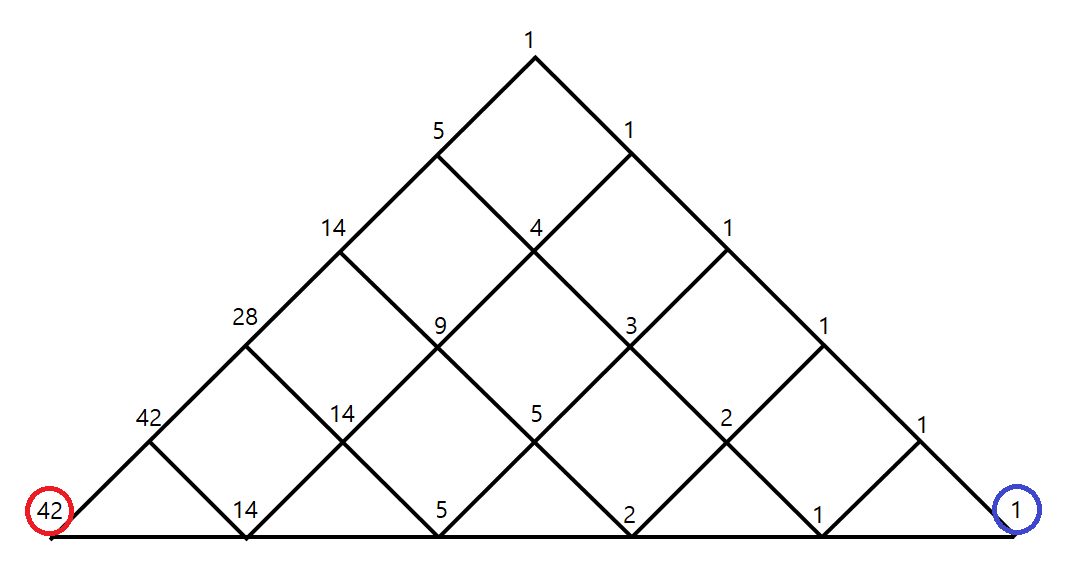
위의 그림은 카탈란 수를 설명할 때 주로 사용되는 그림입니다. 가장 오른쪽을 1로 두고 경우의 수를 구합니다. n*m 격자에서 경로의 경우의 수를 구하는 방식과 유사하게 구합니다. 이렇게 구해놓으면, k번째 괄호 문자열을 구할 수 있습니다.

방식은 이렇습니다. 빨간색으로 표시된 왼쪽 모서리에서 시작합니다. 각 단계마다 k와 오른쪽 상단의 수를 비교합니다. k가 상단의 수 이하라면 위쪽으로, 크다면 k에서 상단의 수를 빼고 아래쪽으로 이동합니다. 이때 위쪽으로 이동했으면 ‘(‘를, 아래쪽으로 이동했으면 ‘)’를 출력합니다. 파란색으로 표시된 오른쪽 모서리에 도착할 때까지 반복하면 k번째 괄호 문자열을 출력하게 됩니다.

이 방식이 k번째 괄호 문자열을 출력하는 이유는 다음과 같습니다. 어떤 꼭짓점에서 오른쪽 상단에 적힌 숫자는 그곳으로 가는 경로의 개수입니다. 마찬가지로 오른쪽 하단에 적힌 숫자도 그곳으로 가는 경로의 개수입니다. 예를 들어, 왼쪽 모서리에서 출발하여 오른쪽 상단으로 이동하고 ‘(‘ 하나를 출력한 상태일 때, 위쪽으로 가는 경우의 수는 28개이고, 아래쪽으로 가는 경우의 수는 14개입니다.

이때 k에 따라 위쪽과 아래쪽을 선택할 수 있습니다. 예시의 상황에서 k가 10이라면 위쪽으로 가야 합니다. 왜냐하면 28개가 ‘(‘로 시작하고 14개가 ‘)’로 시작하기 때문입니다. 비슷하게 k가 35일때는 아래쪽으로 가야합니다.

아래쪽으로 갈때 k에서 오른쪽 상단의 수를 빼주는 이유는, 이전 상태에서는 k번째이지만 ‘)’로 시작하는 문자열에서는 k-(‘(‘로 시작하는 문자열의 개수)번째이기 때문입니다.

이제 위의 격자를 배열로 만들고 알고리즘을 잘 구현하면 됩니다. 주의할 점으로 k가 0부터 시작하므로 1을 더해주었고, 최대 개수보다 k가 크다면 -1을 출력하고 프로그램을 종료시켰습니다.

#include<stdio.h>
long long n,k,s[30][30];
int main()
{
	scanf("%lld%lld",&n,&k); n/=2; k++;
	s[1][0]=1;
	for(int i=1;i<=n+1;i++)
		for(int j=i;j<=n+1;j++)
			s[i][j]=s[i][j-1]+s[i-1][j];

	int x=n,y=n+1;
	if(k>s[x][y]) { printf("-1"); return 0; }
	while(y>1)
	{
		if(k<=s[x][y]) printf("("),x--;
		else printf(")"),k-=s[x][y],y--;
	}
}