Network Flow Algorithm 1 - CyberFlower Algorithm

Network Flow 알고리즘은 가중치가 있는 방향그래프에서 간선의 용량에 맞게 S(Source)에서 T(Synk)로 흐를 수 있는 최대 유량을 묻는 문제이다. 아래 그림을 보자.

플로우 예시

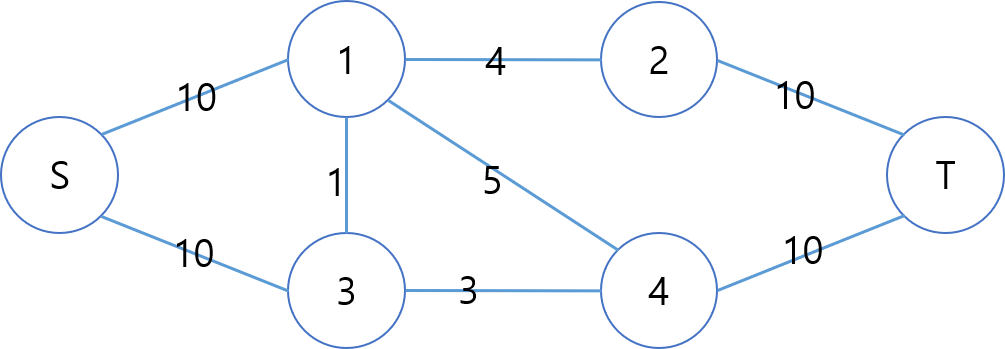
S에서 T로 흐를 수 있는 최대 유량은 12이다. 1-2에서 4, 1-4에서 5, 3-4에서 3만큼 흐를 수 있다.

Network Flow Algorithm 중 가장 기초적인 알고리즘은 Ford-Fulkerson 알고리즘과 Edmond Karp알고리즘이라고 할 수 있다. 이 두 알고리즘은 탐색 방식의 차이(dfs와 bfs) 말고는 차이가 크지 않지만 시간 복잡도가 달라 상황에 알맞은 식을 써야 한다.

플로우 알고리즘은 난이도가 쉬운 알고리즘은 아니다. 이해가 잘 안 되더라도 여러번 읽고 생각해보기를 추천한다.

Network Algorithm 용어 정리

source(S), synk(T)
capacity(용량): c(a,b)로 표현하며 간선 ab에서 최대로 흐를 수 있는 flow의 양
flow(유량): f(a,b)로 표현하며 간선 ab에서 현재 흐르는 유량의 크기
residual capacity(잔여 용량): cf(a,b)로 표현하며 c(a,b)-f(a,b)

Network Algorithm 개관

Ford-Fulkerson과 Edmond Karp알고리즘은 공통적으로

S에서 T로 가는 경로를 하나 찾는다. (dfs: F.F, bfs: E.K)
해당 경로에서 가장 작은 capacity c를 찾는다.
c만큼 경로에 flow를 흘려준다. 잔여 용량을 update한다.

의 작업을 반복한다.

이러한 알고리즘을 위해 우리는 f(a,b)=-f(b,a) 라는 아이디어를 정의한다. b에서 a로 흐르는 유량은 a에서 b로 흐르는 유량의 음의 값이라는 말이다.

논리적으로 생각하면 당연한 말이지만 왜 많은 사람들이 플로우에서 저 식이 중요하다고 하는지, 어디에 저 아이디어가 쓰인다는 건지 필자는 처음에 파악하기 힘들었다.

플로우 예시2

S-1-3-4-T 경로를 보자. 우리는 이 경로를 탐색하면서 1이라는 유량을 보내줄 것이다. 하지만 실제로 S에서 T로 유량을 많이 보내기 위해서 1-3에 1을 보내지는 않는다.

이 경로에서 cf(1,3)-=1을 해주고 cf(3,1)에는 +1을 해주자. 잔여유량이 +1이 되면서 언젠가 나타날 다음 탐색에서 3에서 1로 1만큼의 플로우가 흐른다면 이는 애초에 1-3에서 플로우가 흐르지 않은 것과 같다. 이를 설명하기 위해 f(1,3)=-f(3,1)이라는 이야기가 나온것이다. (1이 3에게 빚을 졌다고 생각해도 좋다. 3은 1이 빚을 진 만큼만 플로우를 보낼수도 있고, 더 보낼수도 있다.)

Ford-Fulkerson 알고리즘 (dfs 탐색, 시간 복잡도 O(EF))

#include<bits/stdc++.h>
using namespace std;
const int SZ=105;
vector<int> graph[SZ];
int cf[SZ][SZ];
int vst[SZ];
int src,synk;
int dfs(int x, int mnc){
  vst[x]=1;
  if(x==synk) return mnc;
  for(auto nxt:graph[x]){
    if(vst[nxt]==1 || cf[x][nxt]<=0) continue;
    int f=dfs(nxt,min(cf[x][nxt],mnc));
    if(f>0){
      cf[x][nxt]-=f;
      cf[nxt][x]+=f;
      return f;
    }
  }
  return 0;
}
int flow(){
  int ans=0;
  while(1){
    memset(vst,0,sizeof(vst));
    int f=dfs(src,INT_MAX);
    if(f==0) break;
    ans+=f;
  }
  return ans;
}

dfs 탐색을 한 번 할때마다 해당 경로에서 가장 작은 capacity 만큼의 플로우가 흐르므로, 최악의 경우 탐색을 총 F번(최대로 흐를 수 있는 유량) 하게 된다. 한번 탐색하는데 E만큼의 복잡도가 필요하므로 시간복잡도는 O(EF)가 된다.

Edmond Karp 알고리즘 (bfs 탐색, 시간복잡도는 O(VE^2))

#include<bits/stdc++.h>
using namespace std;
const int SZ=105;
vector<int> graph[SZ];
int cf[SZ][SZ];
int vst[SZ];
int par[SZ];
int src,synk;
int bfs(){
  queue<int> q;
  q.push(src); vst[src]=1; par[src]=-1;
  while(!q.empty()){
    int x=q.front(); q.pop();
    if(x==synk) break;
    for(int nxt:graph[x]){
      if(vst[nxt]==1 || cf[x][nxt]<=0) continue;
      q.push(nxt); vst[nxt]=1; par[nxt]=x;
    }
  }
  if(vst[synk]==0) return 0;
  int p=synk, mn=INT_MAX;
  while(par[p]!=-1){
    mn=min(mn,cf[par[p]][p]);
    p=par[p];
  }
  p=synk;
  while(par[p]!=-1){
    cf[par[p]][p]-=mn;
    cf[p][par[p]]+=mn;
    p=par[p];
  }
  return mn;
}
int flow(){
  int ans=0;
  while(1){
    memset(vst,0,sizeof(vst));
    int f=bfs();
    if(f==0) break;
    ans+=f;
  }
  return ans;
}

Edmond Karp알고리즘의 시간복잡도는 koosaga님 블로그에 깔끔하게 증명되어 있으니 참고해도 좋을 것 같다. https://koosaga.com/133

아직 Network Flow Algorithm 은 많이 남았다. 이어서 보려면 Network Flow Algorithm 2 를 참고하라.