Bipartite Matching, Konig’s Theorem
이번 게시물에서는 Ford Fulkerson 알고리즘을 최적화 한 코드를 소개할 예정이므로 여기에서 F.F와 E.K를 보고 오는 것도 좋습니다.
이분 매칭(Bipartite Matching) 이란 이분 그래프에서 최대 매칭(Maximum Matching)의 개수를 구하는 문제입니다.
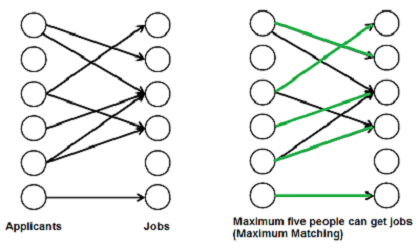
geeksforgeeks 에서 가져온 이분매칭을 설명하기 위한 그림입니다. 위의 그래프처럼 왼쪽 그룹에서 오른쪽 그룹으로 가는 간선은 있지만 왼쪽 그룹 내에서, 오른쪽 그룹 내에서 서로 연결하는 간선이 없는 그래프를 이분 그래프(Bipartite Graph) 라고 합니다.
그림처럼 여러명의 지원자와 직업이 있는 상황을 가정해봅시다. 우리는 하나의 지원자는 하나의 직업을 갖고, 하나의 직업은 하나의 지원자만을 받으면서도 가능한 많은 지원자들이 직업을 갖는 최대 지원자의 수를 알고 싶습니다. 이러한 상황을 이분 매칭이라 합니다.
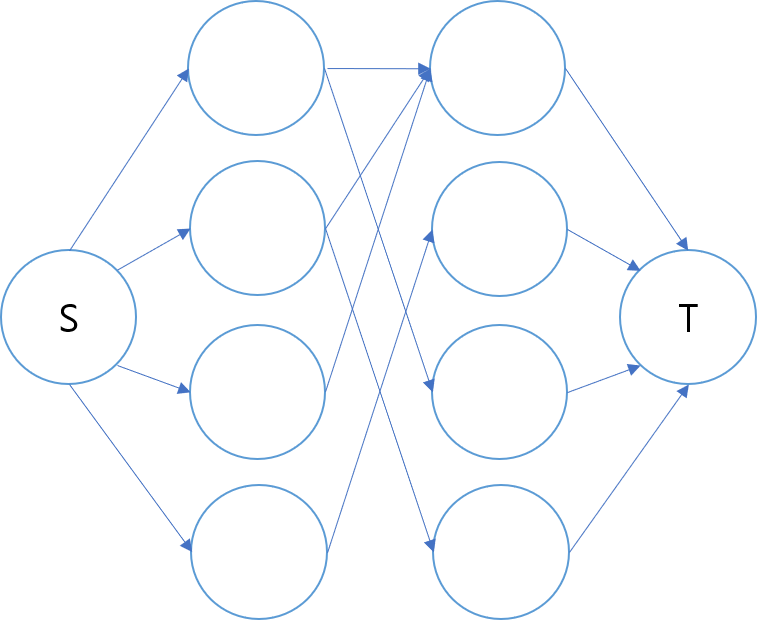
위 그림처럼 왼쪽에 source(S)를, sink(T)를 추가하고 모든 간선을 1이라고 생각하면 단순 플로우 문제로 바뀝니다. 지원자나 직업 모두 1이상의 유량이 흐르지 않기 때문입니다. 따라서 우리는 Ford Fulkerson 알고리즘을 이용하면 O(EF)=O(EV)의 시간복잡도를 갖습니다.
Ford Fulkerson을 그대로 이용한 이분매칭 (복잡도 O(EV))
Ford Fulkerson을 이용하여 백준 2188 축사 배정 문제를 풀어보도록 하겠습니다.
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int SZ=205;
vector<int> graph[2*SZ];
int cf[2*SZ][2*SZ];
int vst[2*SZ];
int src,snk;
int dfs(int x, int mnc){
vst[x]=1;
if(x==snk) return mnc;
for(int nxt:graph[x]){
if(vst[nxt]==1 || cf[x][nxt]<=0) continue;
int f=dfs(nxt,min(cf[x][nxt],mnc));
if(f>0){
cf[x][nxt]-=f;
cf[nxt][x]+=f;
return f;
}
}
return 0;
}
int ford_fulkerson(){
int ans=0;
while(1){
memset(vst,0,sizeof(vst));
int f=dfs(src,INT_MAX);
if(f==0) break;
ans+=f;
}
return ans;
}
int main(void){
ios::sync_with_stdio(false); cin.tie(NULL);
int n,m; cin>>n>>m;
src=0; snk=n+m+1;
for(int i=1;i<=n;i++){
graph[src].pb(i);
cf[src][i]=1;
graph[i].pb(src);
}
for(int i=n+1;i<=n+m;i++){
graph[i].pb(snk);
cf[i][snk]=1;
graph[snk].pb(i);
}
for(int i=1;i<=n;i++){
int x; cin>>x;
for(int j=0;j<x;j++){
int y; cin>>y;
graph[i].pb(n+y);
cf[i][n+y]=1;
graph[n+y].pb(i);
}
}
cout<<ford_fulkerson();
return 0;
}
왠지 불필요한 코드가 많아 보입니다. 코드의 길이와 실행 시간을 단축시킬 수 있을까요? 이분매칭 조건들을 이용하여 최적화를 시켜봅시다.
약간의 최적화가 추가된 이분매칭 (복잡도 O(EV))
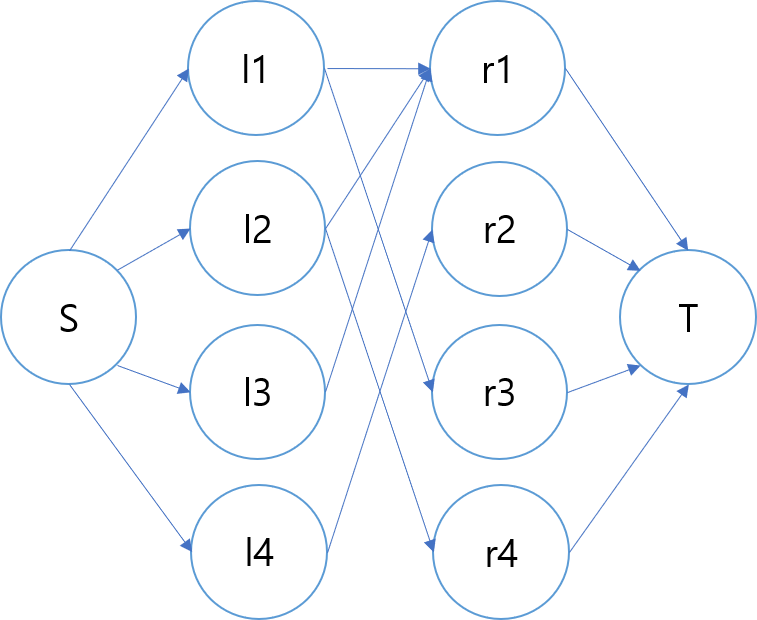
$ s \rightarrow l_1 \rightarrow r_1 \rightarrow t \rightarrow r_1 \rightarrow l_1 \rightarrow s \rightarrow l_2 \rightarrow r_4 \rightarrow t … $
dfs 과정을 따라가 보았습니다. 다시 보니 s,t 과정이 필요 없어 보이는데 반해 비중이 너무 큽니다. ford_fulkerson을 간추릴 수 있을 듯 합니다.
$ l_1 $ 부터 시작해서 물을 흘려 봅니다. $ l_x $ 에서 물을 흘릴 때, 지금까지 흐르던 물들의 방향을 바꿔서라도 $ l_x $에서 어딘가로 추가적으로 물을 흘릴 수 있다면 matching은 1 증가합니다.
즉,
- $ l_1 \rightarrow r_1 $ : true
- $ l_2 \rightarrow r_4 $ : true
- $ l_3 \rightarrow r_1 $, $ r_1 \rightarrow l_1 $, $ l_1 \rightarrow r_3 $ : true
- $ l_4 \rightarrow r_2 $ : true
따라서 이분매칭은 4입니다.
이제 간단하고 빨라진 코드로 백준 11375 열혈강호 문제를 풀어보도록 하겠습니다.
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int SZ=1005;
vector<int> graph[SZ];
int vst[2*SZ];
int mch[2*SZ];
int n,m;
bool dfs(int x){
vst[x]=1;
for(int nxt:graph[x]){
if(vst[mch[nxt]]==1) continue;
if(mch[nxt]==0 || dfs(mch[nxt])){
mch[nxt]=x;
mch[x]=nxt;
return true;
}
}
return false;
}
int bimatch(){
int ans=0;
for(int i=1;i<=n;i++){
memset(vst,0,sizeof(vst));
if(dfs(i)) ans++;
}
return ans;
}
int main(void){
ios::sync_with_stdio(false); cin.tie(NULL);
cin>>n>>m;
for(int i=1;i<=n;i++){
int x; cin>>x;
for(int j=0;j<x;j++){
int y; cin>>y;
graph[i].pb(n+y);
}
}
cout<<bimatch();
return 0;
}
코드도 훨씬 간단해졌습니다. 디닉의 알고리즘(Dinic’s Algorithm) 을 이용하면 이분매칭의 시간복잡도를 $ O(\sqrt{V}E) $ 까지 줄일수 있는데 이를 Hopcroft–Karp algorithm이라고 합니다. 이는 디닉의 알고리즘을 정리한 후에 빠른 시일내로 업로드 하겠습니다.
Minimum Vertex Cover, Konig’s Theorem
이분매칭(이분 그래프에서 최대 매칭)은 minimum vertex cover와 같다는 정리입니다. 일반적인 그래프에서 minimum vertex cover의 개수를 구하는 문제는 NP Hard이기 때문에 이분그래프에서 Konig’s Theorem은 굉장히 획기적인 정리라고 할 수 있습니다.
그렇다면 Minimum Vertex Cover는 무엇일까요? 복도(간선)와 방(정점)으로 이루어진 그래프가 있다고 생각해 봅시다. 또, 방에 경비원을 배치하면 경비원이 방과 연결되어 있는 모든 복도를 감시할 수 있다고 가정해 봅시다.
여기서 Vertex Cover란 배치해야 하는 경비원의 수를 의미하며, Minimum Vertex Cover는 모든 복도를 감시하기 위해 필요한 최소 경비원의 수를 의미합니다.
Minimum Vertex Cover를 안다면 쉬운 문제가 있으니 백준 17402 풀이 이 글을 참고하는 것도 좋을 것 같습니다.
