백준 13511 트리와 쿼리 2
1번 쿼리 :
- 탐색을 하면서, 루트에서 노드까지 가는 모든 비용을 저장해 둡시다.
- 거리를 구했던 방법과 동일하게 구할 수 있습니다.
2번 쿼리:
- 문제에서 k가 y+z 이하임을 보장하고 있습니다.
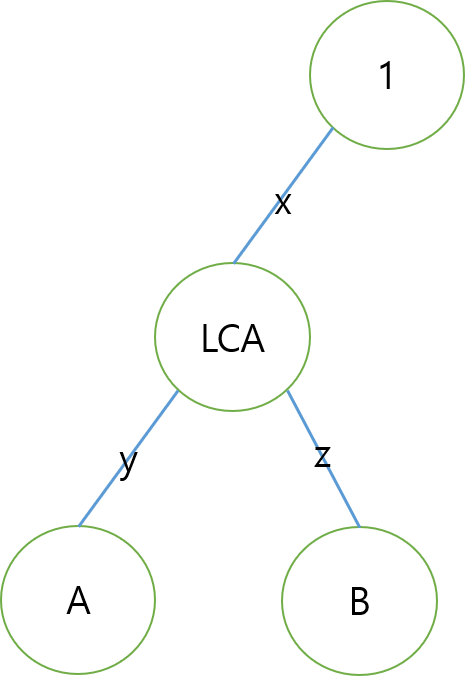
- A에서 B로 가는 경로에서 k번째 노드를 찾는 쿼리를 생각해봅시다.
- k가 y 이하라면 우리는 A에서 k만큼 레벨업 하면 됩니다.
- k가 y 이상이라면 우리는 B에서 (y+z-k)만큼 레벨업 하면 됩니다.
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
typedef long long ll;
const int SZ = 100005;
const int MXH = 18;
vector<pii> graph[SZ];
int dp[MXH][SZ];
ll dist[SZ];
int lv[SZ];
void dfs(int crt, int prt, int level, ll dst){
lv[crt]=level;
dp[0][crt]=prt;
dist[crt]=dst;
int l = graph[crt].size();
for(int i=0;i<l;i++){
int nxt = graph[crt][i].first; int w = graph[crt][i].second;
if(nxt!=prt) dfs(nxt,crt,level+1,dst+(ll)w);
}
}
int level_up(int x, int k){
for(int i=0;i<MXH;i++){
if((1<<i)&k) x=dp[i][x];
}
return x;
}
int lca(int a, int b){
int na = level_up(a,max(lv[a]-lv[b],0));
int nb = level_up(b,max(lv[b]-lv[a],0));
for(int i=MXH-1;i>=0;i--){
if(dp[i][na]!=dp[i][nb]){
na = dp[i][na];
nb = dp[i][nb];
}
}
if(na!=nb){
na = dp[0][na];
nb = dp[0][nb];
}
return na;
}
int main(void){
int n; scanf("%d",&n);
for(int i=1;i<n;i++){
int a,b,c; scanf("%d %d %d",&a,&b,&c);
graph[a].push_back(make_pair(b,c));
graph[b].push_back(make_pair(a,c));
}
dfs(1,0,0,0);
for(int i=1;i<MXH;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i-1][dp[i-1][j]];
}
}
int m; scanf("%d",&m);
for(int i=0;i<m;i++){
int q; scanf("%d",&q);
if(q==1){
int a,b; scanf("%d %d",&a,&b);
int na = lca(a,b);
printf("%lld\n",dist[a]+dist[b]-2*dist[na]);
}
else if(q==2){
int a,b,c; scanf("%d %d %d",&a,&b,&c);
c--;
int na = lca(a,b);
int x = lv[a]-lv[na];
int y = lv[b]-lv[na];
if(c<x) printf("%d\n",level_up(a,c));
else printf("%d\n",level_up(b,y+x-c));
}
}
return 0;
}
