백준 1761 정점들의 거리
https://www.acmicpc.net/problem/2233
LCA와 LCA 도중에 나오는 level을 이용하면 쉽게 구할 수 있습니다.
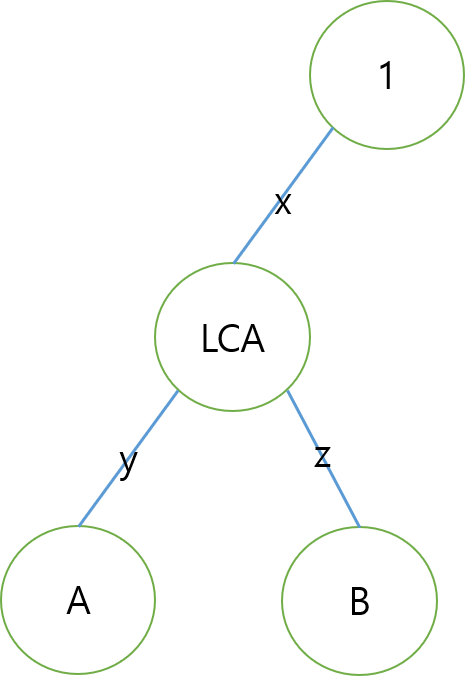
0 base-level이 1에서부터의 거리이기 때문에
dist(a,b)=level[a]+level[b]-2level[LCA(a,b)]입니다. (y+z=(x+y)+(x+z)-2x)
자, 구현을 시작하죠!
#include<bits/stdc++.h>
#define SZ 40005
#define MX_H 20
using namespace std;
typedef pair<int,int> pii;
vector<pii> graph[SZ];
int lv[SZ];
int dp[MX_H][SZ];
int dis[SZ];
void dfs(int cur, int prt, int level, int dist){
dis[cur] = dist;
lv[cur] = level;
dp[0][cur] = prt;
int l = graph[cur].size();
for(int i=0;i<l;i++){
int next = graph[cur][i].first; int ndis = graph[cur][i].second;
if(prt!=next) dfs(next,cur,level+1,dist+ndis);
}
}
int level_up(int x, int d){
for(int i=MX_H-1;i>=0;i--){
if(d&(1<<i)) x=dp[i][x];
}
return x;
}
int main(void){
int n; scanf("%d",&n);
for(int i=0;i<n-1;i++){
int a,b,c; scanf("%d %d %d",&a,&b,&c);
graph[a].push_back(make_pair(b,c));
graph[b].push_back(make_pair(a,c));
}
dfs(1,0,0,0);
for(int i=1;i<MX_H;i++){
for(int j=1;j<=n;j++){
dp[i][j]=dp[i-1][dp[i-1][j]];
}
}
int m; scanf("%d",&m);
for(int i=0;i<m;i++){
int x,y; scanf("%d %d",&x,&y);
int nx = level_up(x,max(lv[x]-lv[y],0));
int ny = level_up(y,max(lv[y]-lv[x],0));
for(int i=MX_H-1;i>=0;i--){
if(dp[i][nx]!=dp[i][ny]){
nx=dp[i][nx];
ny=dp[i][ny];
}
}
if(nx!=ny){
nx = dp[0][nx]; ny = dp[0][ny];
}
printf("%d\n",dis[x]+dis[y]-2*dis[nx]);
}
return 0;
}
