Convex Hull Trick - CyberFlower Algorithm

Convex Hull Trick Algorithm

동아리 알고리즘 세미나에서 후배님이 CVT를 주제로 세미나를 진행하셨고, 덕분에 저도 미루고 미루던 CVT 알고리즘에 대한 글을 정리하게 되었습니다.

DP optimization 중 하나인 Convex Hull Trick에 대하여 알아보겠습니다.

$ DP[i]=MIN(a_j x_i+DP[j]) (1 \leq i \leq i-1) $ 에 해당하는 DP문제가 있을때,

$ a_j $ 가 감소수열이라면 우리는 해당 DP 문제를 O(n) 또는 O(nlogn)으로 해결할 수 있습니다.

(해당 조건이 없다면 $ O(n^2) $ 복잡도가 필요합니다.)

$ x_i $ 가 증가수열 (복잡도 $ O(n) $)

우리는 DP[j]를 y 절편으로 하고 $ x_i $ 를 x축, 기울기를 $a_j$으로 하는 2차원 그래프를 생각할 수 있습니다.

가장 작은 값을 구하는 문제이므로 가장 작은 선들을 취한다면 convex hull(볼록 다각형)의 모양을 갖게 됩니다.

CHT

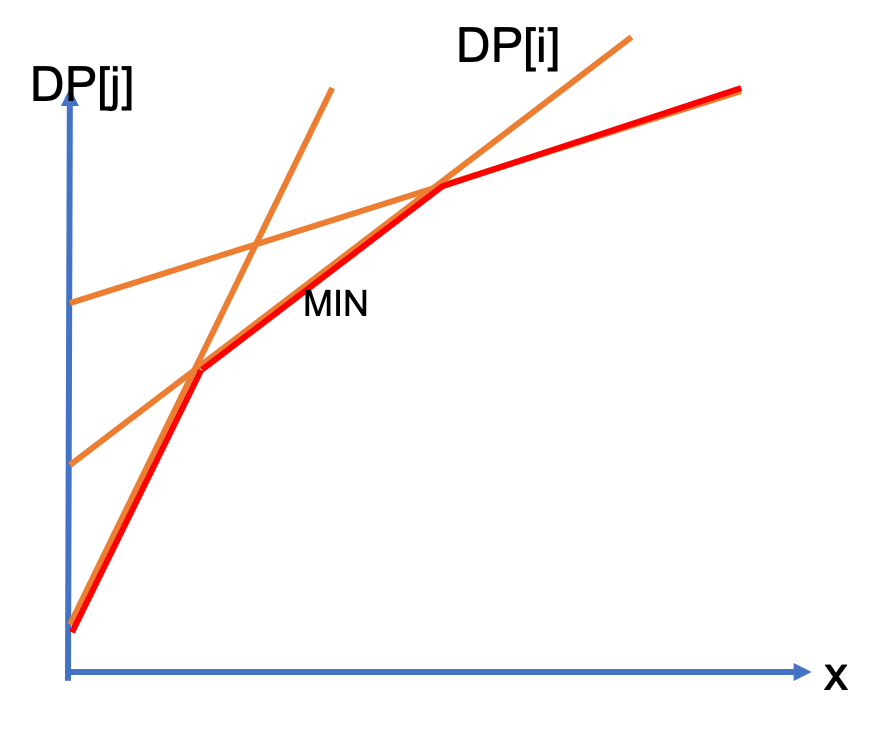
따라서 우리는 새로운 직선이 추가될때 마다 볼록다각형을 이루는 직선을 O(1)에 저장할 수 있습니다. (절편과 기울기를 덱에 저장하면 됩니다.)

아래 그림과 같은 경우를 생각해봅시다. 1,2,3의 순서로 직선이 생기는데, 직선 2는 MIN을 구하는데 필요가 없고 제거해도 됩니다. (직선 3과 1의 교점이 직선 3과 2의 교점보다 더 왼쪽에 위치하고, 따라서 MIN 선분들에 포함되지 않습니다.) 따라서 이러한 경우에는 pop을 해주면 됩니다.

CHT

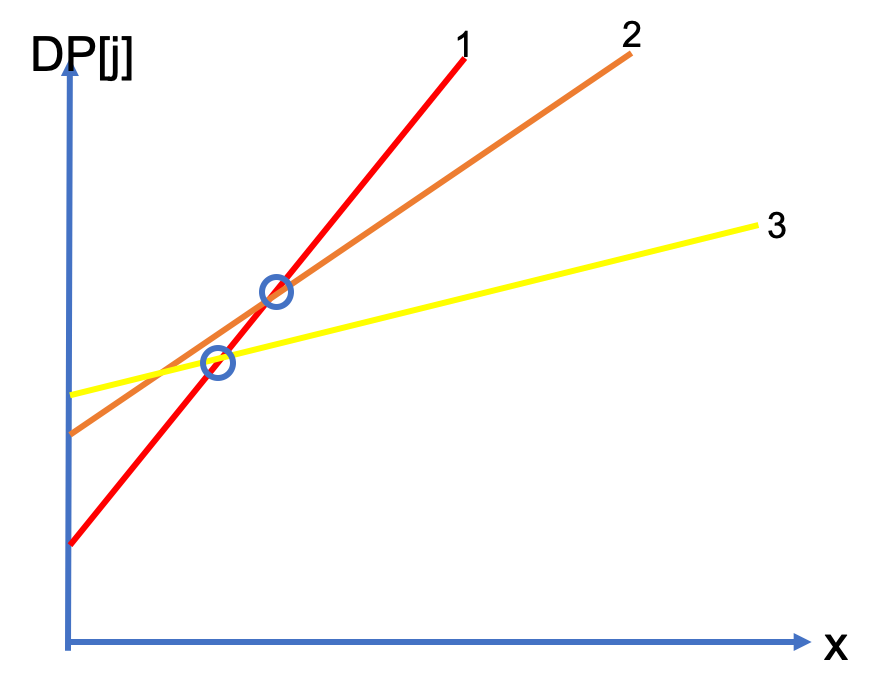
마지막으로, $ x_i $가 증가수열이므로 $ x_i $ 를 찾는 수고를 들일 필요 없습니다.

자세한 구현은 코드를 통해 살펴보도록 하겠습니다.

class CVT{
private:
    deque<pll> lne;
    vector<ll> memo;
    double crs(pll l1, pll l2){
        return (double)(l2.second-l1.second)/(double)(l1.first-l2.first);
    }
public:
    CVT(int n){
        memo.resize(n,0);
    }
    ll query(int i, ll x, ll a){
        // 1. pop edges if range is less than x
        while(lne.size()>1 && crs(lne[0],lne[1])<x){
            lne.pop_front();
        }
        // 2. first edge include x by 1
        if(i) memo[i]=x*lne[0].first+lne[0].second;   
        else memo[i]=0;     
        // 3. pop edges NOT in convex hull
        while(lne.size()>1 && crs(lne[lne.size()-1],lne[lne.size()-2])>=crs(lne[lne.size()-1],{a,memo[i]})){
            lne.pop_back();
        }
        // 4. push new line
        lne.push_back({a,memo[i]});
        return memo[i];        
    }
};

1: x가 증가수열이므로, x보다 작은 range에 있는 convex hull은 볼 필요가 없습니다. 날려줍시다.

3: 새로 들어온 직선으로 인하여 convex hull에서 빠지게 되는 직선들이 존재했습니다. pop해줍시다.

4: 새로 들어온 직선을 push 해줍니다.

$ x_i $ 의 규칙이 없는 경우 ($ O(nlogn) $)

$ x_i $가 증가수열이라면 위의 코드를 이용하면 O(1)의 복잡도가 필요하지만, $ x_i $의 규칙을 모른다면 이분탐색으로 해당하는 선분을 찾는 방법 뿐입니다.