Fast Fourier Transform - CyberFlower Algorithm

Fast Fourier Transform (FFT) Algorithm

일단 제 글에서는 FFT 관련 알고리즘 문제를 해결하기 위한 최소한의 지식만을 소개하고 있음을 알립니다. 보다 더 엄밀하고 정확한 수학적인 내용을 원하신다면 다른 블로그를 보셔야 해요!!

많이 어려운 알고리즘이였고, 따라서 정말 많은 출처를 참고하였습니다. 주로 ansemddle97 선배님의 설명과 코드, https://topology-blog.tistory.com/6 블로그의 설명과 일부 코드, https://casterian.net/archives/297의 수학 설명들을 매우 많이 참고하였음을 미리 밝힙니다. (ansemddle97 선배님 늘 감사드려요!!)

필요한 수학적 지식을 시작으로 FFT 알고리즘 소개를 시작하도록 하겠습니다.

FFT 개관

알고리즘에서 FFT는 합성곱(convolution)을 빠르게 구하는데 유리합니다. 예를 들어 polynomial한 두 다항식의 곱을 생각해볼 수 있습니다.

$ a_0x^0+a_1x^1+…+a_nx^n $ 과 $ b_0x^0+b_1x^1+…+b_mx^m $을 곱하려면 시간복잡도가 $ O(nm) $ 이 됩니다. 하지만 FFT를 사용한다면 $ O(nlogn), if(n>m) $의 시간복잡도로 해결할 수 있게 됩니다.

이제 위의 두 다항식을 빠르게 곱하는 코드 작성을 목표로 설명을 진행하겠습니다.

수학 보조정리

보조정리 1. $ e^{i\theta}=cos\theta+isin\theta $
보조정리 2. Fourier의 정리 허수 수열 $ \phi_k(n) $을
\[\phi_k(n)=\{ {e^{0*ik\theta}}, {e^{1*ik\theta}}, ... ,{e^{(n-1)* ik\theta}} \}\]
이라고 합시다. ($ \theta=\frac{2\pi}{n} $)

Fourier 정리에 의하여 $ \phi_0(n), \phi_1(n), … \phi_{n-1}(n) $ 을 기저로 하여 모든 n차 합성함수를 표현할 수 있습니다. (으악)
보조정리 3. 복소벡터 $ \phi_{k1}(n) $,$ \phi_{k2}(n)$ 에서 $ k_1 $ 과 $ k_2 $ 가 다르면 두 복소벡터는 직교합니다.

pf) 복소벡터의 내적을 해보겠습니다.
\[\sum_{j=0}^{j=n-1}{e^{j*i(k_1-k_2)\theta}}= \frac{e^{ni(k_1-k_2)\theta}-1}{e^{ik\theta}-1}=0\]
이므로 증명되었습니다.
보조정리 4. 퓨리에 변환 수열 $ a={ a_0, … ,a_{n-1} } $ 이라고 하면 $\phi_k$에 대한 퓨리에 변환은
\[A_k=\sum_{j=0}^{j=n-1} a_je^{j*ik\theta}\]
라고 하고, $ A={A_0,…A_{n-1}} $ 이라 하겠습니다.
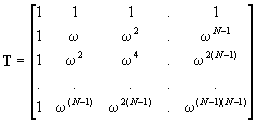
보조정리 5. 역행렬 위에서 제시한 퓨리에 변환 행렬을 생성할 수 있으며, 이 행렬은 역행렬이 존재합니다. 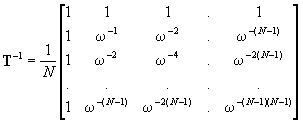선형대수학의 내용이니 증명은 생략하겠습니다.

알고리즘 개관

a+b 이상 적당히 큰 2의 거듭제곱꼴의 n을 찾고, a,b를 길이가 n인 수열로 변환(0 추가)
수열 a,b를 A,B로 변환
C를 O(n)으로 계산 (보조정리 3을 통해 $C_k=A_kB_k$ 임을 알 수 있음)
C를 c로 변환 (보조정리 5)

편의를 위해서 n은 2의 거듭제곱을 가정합니다. n이 a,b보다 길때는 0을 채워넣으면 되고, n이 1일때는 c=a*b이므로 걱정할 필요가 없습니다.

n이 짝수이므로

\[A_k= \sum_{j=0}^{j=n-1} a_je^{j*ik \theta} = \sum_{j=0}^{j=n/2-1} a_{2j}e^{j*ik \theta_1} + e^{ik \theta} \sum_{j=0}^{j=n-1} a_{2j+1}e^{j*ik \theta_1}\]

라는 식이 나옵니다. ( $ \theta_1=\frac{2\pi}{\frac{n}{2}} $ )

전체와 부분의 모양이 비슷하므로 우리는 이 식을 통해서 분할정복을 이용할 수 있습니다. 또, $A_k=A_{(k+n/2)}$라는 식도 유추할 수 있겠군요.

방금 소개한 식을 이용하여 분할정복을 진행합니다.

자리수가 300,000 정도 되는 큰 두수를 곱하는 것도 FFT로 해결이 가능합니다. x대신 10을 인자로 갖는 다항식이라고 생각하면 되기 때문이죠.

큰 수 곱셈, 큰 수 곱셈(2)를 풀어보겠습니다.

#include <bits/stdc++.h>
using namespace std;
// 복소수 자료형을 정의
typedef vector<int> vi;
typedef complex<double> base;
string s,t;
class FFT_multi{
private:
  int n,sn,tn;
public:
  FFT_multi(){
    sn=s.size();
    tn=t.size();
    n=1;
    while(n<sn+tn) n<<=1;
  }
  void fft(vector<base> &dst, vector<base> &arr, int ln, bool inv){
    dst.resize(ln,0);
    if(ln==1){
      dst[0]=arr[0];
      return;
    }
    vector<base> a,b;
    for(int i=0;i<ln/2;i++){
      a.push_back(arr[2*i]);
      b.push_back(arr[2*i+1]);
    }
    vector<base> A,B;
    fft(A,a,ln/2,inv);
    fft(B,b,ln/2,inv);
    double angle=inv?(-2*M_PI/ln):(2*M_PI/ln);
    base w=base(cos(angle),sin(angle));
    base twiddle_factor=base(1,0);
    for(int i=0;i<ln/2;i++){
      dst[i]=A[i]+twiddle_factor*B[i];
      dst[i+ln/2]=A[i]-twiddle_factor*B[i];
      twiddle_factor*=w;
    }
  }
  vi multiply(){
    vi ret(n+1,0);
    vector<base> x,y;
    for(int i=0;i<n;i++){
        if(i<sn) x.push_back(base(s[sn-i-1]-'0',0));
        else x.push_back(base(0,0));
        if(i<tn) y.push_back(base(t[tn-i-1]-'0',0));
        else y.push_back(base(0,0));
    }
    vector<base> v1,v2,ans;
    fft(v1,x,n,true);
    fft(v2,y,n,true);
    for(int i=0;i<n;i++) v1[i]=v1[i]* v2[i];
    fft(ans,v1,n,false);
    for(int i=0;i<n;i++) ans[i]/=n;
    for(int i=0;i<n;i++){
        ret[i]+=(int)round(ans[i].real());
        ret[i+1]+=ret[i]/10;
        ret[i]%=10;
    }
    reverse(ret.begin(),ret.end());    
    return ret;
  }
};
int main(void){
  ios_base::sync_with_stdio(false); cin.tie(NULL);
  cin>>s>>t;
  if(s.compare("0")==0 || t.compare("0")=='0'){
    cout<<0;
    return 0;
  }
  FFT_multi fft=FFT_multi();
  vi ans=fft.multiply();
    int idx=0;
    while(ans[idx]==0) idx++;  
  for(int i=idx;i<ans.size();i++) cout<<ans[i];
  return 0;
}

하지만 이 코드는 조금 문제가 있었습니다. 시간복잡도는 nlogn이 맞지만, vector의 생성이 너무 많아 생각보다 시간이 오래 걸리더군요. 실제로 위 코드는 큰 수 곱셈에서는 2.5초 통과하지만 큰 수 곱셈(2)에서는 시간제한이 2초인지라 통과하지 못합니다.

비재귀 최적화

재귀함수를 이용하지 않고 FFT를 구할 수 있습니다. 이를 위하여 또 하나의 보조정리를 소개하겠습니다.

보조정리 6. 홀수 번째 수를 앞으로, 짝수 번째 수를 뒤로 빼는 분할정복(=fft 분할정복)에서 i번째 수는 k 자릿수를 뒤집은 수 j번째 위치로 재배열된다.

증명은 수학적 귀납법을 이용하면 할 수 있습니다만… 너무 길어지니 여기서는 굳이 서술하지 않겠습니다. 위에서 말씀드렸던 casterian님 블로그를 참고하시면 좋을 것 같습니다.

나머지는 코드를 보고 설명드리겠습니다.

#include <bits/stdc++.h>
using namespace std;
typedef vector<int> vi;
typedef complex<double> base;
string s,t;
class FFT_multi{
private:
  int n,kk,sn,tn;
  // x에서 k개의 bit를 reverse하는 함수
  inline int bit_reverse(const int x, int k){
    int res=0;
    for(int i=0;i<k;i++){
      res^=((x>>i)&1)<<(k-i-1);
    }
    return res;
  }
public:
  FFT_multi(){
    sn=s.size();
    tn=t.size();
    n=1, kk=0;
    while(n<sn+tn) n<<=1, kk++;
  }
  void fft(vector<base> &arr, bool inv){
    for(int i=0;i<n;i++){
      int j=bit_reverse(i,kk);
      if(i<j) swap(arr[i],arr[j]);
    }
    // 재귀함수의 마지막부터 반복문을 돌리자. 즉, 사이즈가 2일때부터
    for(int i=2;i<=n;i<<=1){
      double angle=inv?(-2*M_PI/i):(2*M_PI/i);
      base w=base(cos(angle),sin(angle));
      for(int j=0;j<n;j+=i){
        base twiddle_factor=base(1,0);
        for(int k=0;k<i/2;k++){
          base tmp=twiddle_factor*arr[j+k+i/2];
          arr[j+k+i/2]=arr[j+k]-tmp;
          arr[j+k]=arr[j+k]+tmp;
          twiddle_factor*=w;          
        }
      }
    }
  }
  vi multiply(){
    vi ret(n+1,0);
    vector<base> x,y;
    for(int i=0;i<n;i++){
        if(i<sn) x.push_back(base(s[sn-i-1]-'0',0));
        else x.push_back(base(0,0));
        if(i<tn) y.push_back(base(t[tn-i-1]-'0',0));
        else y.push_back(base(0,0));
    }
    fft(x,true);
    fft(y,true);
    for(int i=0;i<n;i++) x[i]=x[i]* y[i];
    fft(x,false);
    for(int i=0;i<n;i++) x[i]/=n;
    for(int i=0;i<n;i++){
        ret[i]+=(int)round(x[i].real());
        ret[i+1]+=ret[i]/10;
        ret[i]%=10;
    }
    reverse(ret.begin(),ret.end());    
    return ret;
  }
};
int main(void){
  ios_base::sync_with_stdio(false); cin.tie(NULL);
  cin>>s>>t;
  if(s.compare("0")==0 || t.compare("0")==0){
    cout<<0;
    return 0;
  }
  FFT_multi fft=FFT_multi();
  vi ans=fft.multiply();
    int idx=0;
    while(ans[idx]==0) idx++;  
  for(int i=idx;i<(int)ans.size();i++) cout<<ans[i];
  return 0;
}

FFT, Big Integer Multiply

Fast Fourier Transform (FFT) Algorithm

FFT 개관

수학 보조정리

알고리즘 개관

비재귀 최적화