프로그래머스 10월 챌린지 후기
프로그래머스 월간 챌린지 1회 후기
프로그래머스에서 진행한 월간 챌린지에 참가했습니다. 9월, 10월, 11월에 나누어서 열렸는데 9월은 몰라서 못했고 10월부터 참가했습니다. 11월 프로그래머스는 scpc 본선 2일전에 있었는데 퍼포먼스가 좋지 않았습니다. 덕분에 scpc 본선에서 긴장을 잘 유지했던 것 같기도 해서 다행입니다. :)
첫 대회임에도 문제의 질이 매우 좋았다는 점이 놀라웠고, 닉네임만 봐도 실명을 알 정도의 프로그래밍 고인물들이 스코어보드에 많았다는 점도 놀라웠습니다.(여기까지 와서… 상금을 루팡하셔야겠습니까…ㅋㅋ) 완전한 코드를 짜는 것이 아닌 함수를 짜는 대회라는 점도 신선했습니다. (탑코더도 이러한 방식이라고 하는데, 참가해 본 적은 없습니다.)
3,4번 문제들이 꽤 challenging 했기에 3,4번 문제만 정리해보겠습니다. 1,2번 문제들은 모두 어렵지 않은 구현문제였습니다.
문제는 프로그래머스 사이트에서 확인 가능합니다.
10월 월간 챌린지
3. 트리 트리오 중간값
알고리즘. 트리의 지름을 잡고, 양 끝 점을 $a,b$라고 하면 $max(dist(a,c),dist(b,c))$ 인 $c(c \notin {a,b})$ 을 찾으면 정답입니다.
우리는 중앙값이 적어도 지름 - 1 이 된다는 사실을 쉽게 알 수 있습니다. $a,b$를 지름의 양 끝점으로 하고 $c$를 지름 위의 노드 중에서 $a$와 인접한 노드를 선택하면 됩니다.
하지만 이렇게 되면 중앙값이 지름의 길이가 되는 경우를 확인할 수 없습니다. 즉, 트리의 지름이 여러개 있는 경우는 중앙값이 지름이 될 수 있습니다. 이를 어떻게 처리하는 것이 쉬울까요?
트리의 지름이 여러개라고 가정해봅시다. 즉, 우리는 서로 다른 트리의 지름 끝점 $(a,b),(c,d)$를 생각할 수 있습니다.
지름의 끝 점 쌍들이 모두 disjoint하지 않는다면 우리는 위에서 소개한 알고리즘으로 구현하면 됩니다. 지름의 끝 점 쌍들이 disjoint하다고 가정해봅시다.
$(a,b),(c,d)$ 에 대하여, 우리는 경로 $(a,b)$, $(c,d)$가 만나는 점 $m$을 생각할 수 있습니다.(트리이므로 반드시 존재)
$r==ma+mb==mc+md$ 이며 $ma \neq mb$ 또는 $mc \neq md$ 라면 지름이라는 조건에 모순입니다. 또, 같다면 disjoint하지 않은 새로운 지름 쌍을 만들 수 있습니다.
즉, 우리는 트리의 지름을 잡고 중앙값이 가장 먼 노드를 찾으면 됩니다.
#include <bits/stdc++.h>
using namespace std;
const int SZ=250005;
vector<int> graph[SZ];
int dst1[SZ], dst2[SZ], dst3[SZ];
void dfs(int *dst, int p, int x, int d){
dst[x]=d;
for(int adj:graph[x]){
if(p==adj) continue;
dfs(dst,x,adj,d+1);
}
}
int solution(int n, vector<vector<int>> edges) {
for(auto edge:edges){
int x=edge[0], y=edge[1];
graph[x].push_back(y);
graph[y].push_back(x);
}
dfs(dst1,0,1,0);
int lft=-1, rgt=-1, mx=-1;
for(int i=1;i<=n;i++){
if(mx<dst1[i]){
mx=dst1[i];
lft=i;
}
}
dfs(dst2,0,lft,0);
mx=-1;
for(int i=1;i<=n;i++){
if(mx<dst2[i]){
mx=dst2[i];
rgt=i;
}
}
dfs(dst3,0,rgt,0);
int res=0;
for(int i=1;i<=n;i++){
if(i==lft || i==rgt) continue;
res=max(res,max(dst2[i],dst3[i]));
}
return res;
}
//debug mode in local
#ifdef __TOPCYBERFLOWER
int main(void){
vector<vector<int>> edges;
edges.push_back({1,2});
edges.push_back({2,3});
edges.push_back({3,4});
cout<<solution(4,edges);
return 0;
}
#endif
4. 문자열의 아름다움
대부분의 분들이 fenwick/segment tree로 푸셨던데 저만 수식으로 접근한 것 같습니다. 그래도 제 풀이도 꽤 깔끔한 것 같아 제 풀이를 소개합니다.
일단은 모든 문자의 종류가 다른 문자열을 생각해봅시다. 이 경우를 $f(n), n$은 문자열의 길이라고 합시다.
$ f(n)=\sum_{i=1}^{n}{\sum_{j={i+1}}^n}(j-i)=\frac{(n-1)n(n+1)}{6} $
여기서 우리는 “같은 문자 때문에 생기는 손해”에 대한 식을 구할 수 있습니다.
이해하기 쉽도록, 문자열에서 알파벳 a만 보겠습니다. 일단 baababaaa를 살펴보겠습니다. 그리고 우리는 a로 이루어진 부분문자열만 추출할 겁니다. aa a aaa 이런 식으로 말이죠! 편의상 앞으로 이 부분 문자열들을 $s_i$라고 하겠습니다.
추출된 a에서 손해가 나는 경우는 2가지가 있는데, 첫째는 이어져 있는 a 내부에서 2개 포인터가 선택되는 경우이며 둘째는 서로 다른 두개의 a 부분문자열에서 2개 포인터가 선택되는 경우입니다.
첫째 case는 간단히 처리할 수 있습니다. $ s_i $ 길이만큼 $ f(len(s_i)) $ 를 계산해서 빼주면 됩니다. 우리가 얻었다고 생각한 만큼 고스란히 빠지기 때문이죠.
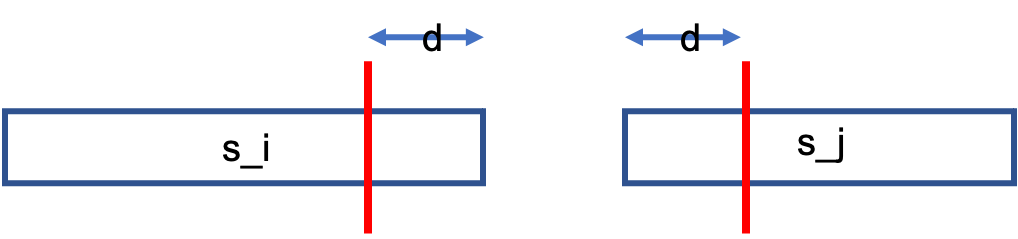
둘째 case에 대해 생각해봅시다. $ s_i \ s_j $ 에 대해서 우리는 손해 값 $d$를 기준으로 생각할 수 있습니다. $ d $가 1인 경우는 $ s_i+s_j-1 $ 이며 일반적인 $ d $에 대하여 $ s_i+s_j-(2d-1), \ d \leq min(len(s_i),len(s_j)) $ 가 됩니다.
즉, 둘째 케이스의 총합은
$ \sum_{s_j \neq s_i}\sum_{d=1}^{d=min(len(s_i),len(s_j))}(d\times (s_i+s_j-(2d-1))) $
가 됩니다.
정렬을 해둔다면, $O(n)$으로 위 식을 깔끔하게 처리할 수 있습니다. 식 전개를 마저 하자면,
$ \frac{len(s_i)(len(s_i)+1)}{2}\times \sum_{s_j}^{s_j \neq s_i} (s_j +\frac{len(s_i)(len(s_i)+1)(1-len(s_i))}{6}) $
이 되기 때문입니다.
따라서 시간복잡도는 정렬에 필요한 $ O(nlogn) $ 입니다.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll all_dif(ll n){
return (n-1ll)*n*(n+1ll)/6ll;
}
inline ll my_func(ll n){
return n*(n+1ll)*(-n+1ll)/6ll;
}
ll solution(string s){
int n=s.size();
ll res=all_dif(n);
for(int i=0;i<26;i++){
vector<ll> alpha;
ll cnt=0;
for(int j=0;j<n;j++){
if(s[j]==i+'a'){
cnt++;
}
else{
if(cnt>0) alpha.push_back(cnt);
cnt=0;
}
}
if(cnt) alpha.push_back(cnt);
int m=alpha.size();
sort(alpha.begin(),alpha.end());
ll sm=0;
for(int j=0;j<m;j++){
res-=all_dif(alpha[j]);
sm+=alpha[j];
}
for(int j=0;j<m;j++){
sm-=alpha[j];
res-=(alpha[j]*(alpha[j]+1ll)*sm/2ll);
res-=((ll)(m-j-1)*my_func(alpha[j]));
}
}
return res;
}
// debug mode in local
#ifdef __TOPCYBERFLOWER
int main(void){
string s; cin>>s;
cout<<solution(s);
return 0;
}
#endif
