Heavy Light Decomposition Algorithm
Heavy Light Decomposition Algorithm
HLD 개관
트리에서 $\text {정점 } u \rightarrow \text {정점 } v$ 로 가는 경로는 유일하다는 특징이 있습니다. 그리고 이러한 경로에 질의를 던지는 쿼리 문제도 상당히 많이 존재합니다.
HLD 알고리즘은 트리를 여러개의 체인으로 나누어 주는 알고리즘입니다. 결론부터 말하자면, 트리에 존재하는 모든 경로에 대해서, 우리는 HLD 알고리즘에서 생성된 체인들 중, $log(n)$개의 체인 정보만을 확인하여 $u \rightarrow v$ 경로에 대한 질의를 처리할 수 있습니다.
이제부터는 HLD 알고리즘이 트리를 체인으로 나누는 방법에 대해 살펴보겠습니다.
Chain Partitioning
HLD chaining의 핵심 원리는 “가장 무거운 chain” 부터 뜯어낸다 입니다. 루트 노드부터 생각해보겠습니다. 루트의 자식이 여러명이라면, 자식들 중에서 가장 자손(=sub-tree의 크기)이 많은 자식은 루트와 같은 체인입니다. 이렇게 탐색하면서, 우리는 트리에서 하나의 chain을 뜯어낼 수 있게 되고, 작은 새로운 트리가 하나 남습니다.
이 방식을 계속 진행하다 보면 언젠가는 트리가 여러개의 chain으로 나누어지게 됩니다. geeks-for-geeks에서 가져온 그림을 보겠습니다. :)
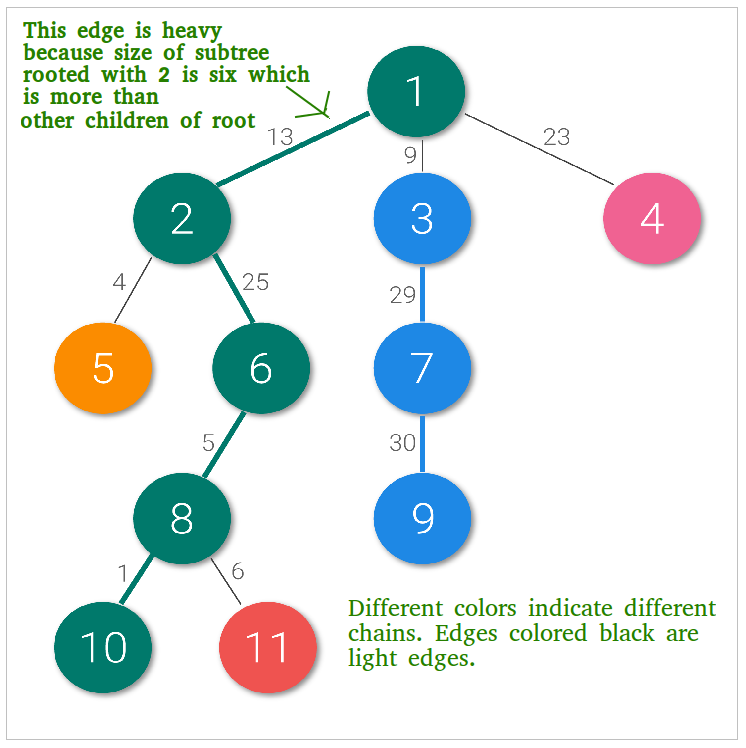
위의 그림에서 트리는 5개의 chain으로 partitioning 되어 있음을 확인할 수 있습니다.
이 chain을 잘 사용하기 위해서는, 하나의 chain 내부 노드들이 모두 연속하는 numbering 이 되어있어야 좋습니다. 여기서 우리는 “ 무거운 체인이 왼쪽에 위치하도록 swap” + “dfs ordering 기법”을 사용하여 원하는 바를 충족할 수 있습니다.
Complexity
임의의 노드 $ r $과 그 자손 노드 $ x $에서 $log(n)$개 이하의 chain만 보면 된다는 것은 쉽게 증명이 가능합니다. ($n_r= r\text{을 루트로 하는 sub tree의 크기}$)
$x$가 가장 왼쪽 chain에 존재한다면 $r$과 $x$는 같은 체인에 존재하게 되고, 아니라면 x가 포함된 나머지 sub tree의 크기는 $n/2$ 이하입니다.
따라서 $r \rightarrow x$로 가는 경로에서 봐야 하는 chain의 수는 재귀적으로 $log(n)$ 이하임이 증명됩니다.
따라서 두 노드 $x,y$에 대하여 $x \rightarrow y$로 가는 경로 chain 수는 $2log(n_{lca}) \leq 2log(V)$ 이하가 됩니다.
구현
HLD 구현체는 chain partitioning까지는 비슷하지만, 쿼리 함수는 응용되는 문제(자료구조)에 따라 달라집니다.
const int SZ=100'005;
vi graph[SZ];
int par[SZ], chi[SZ];
int num[SZ], rev[SZ], grp[SZ];
int tot;
int n;
// calc child_num
// p:parent, x: current node
int init_dfs(int p, int x){
par[x]=p;
chi[x]=1;
for(int adj:graph[x]){
if(adj==p) continue;
chi[x]+=init_dfs(x,adj);
}
return chi[x];
}
// chain partitioning
// g:group number, x:current node
void chain_partitioning(int g, int x){
grp[x]=g; // chain grouping
num[x]=++tot; // dfs ordering
rev[tot]=x;
// pop parent(send back, then pop-back)
// left-most child is same color(group, g) with current node
// other child start new chain
for(int i=0;i<(int)graph[x].size();i++){
int adj=graph[x][i];
if(i!=graph[x].size()-1 && adj==par[x]){
swap(graph[x][i],graph[x].back());
adj=graph[x][i];
}
if(adj!=par[x] && chi[adj]>chi[graph[x][0]]){
swap(graph[x][i],graph[x][0]);
}
}
if(!graph[x].empty() && graph[x].back()==par[x]) graph[x].pop_back();
for(int i=0;i<(int)graph[x].size();i++){
if(i==0) chain_partitioning(g,graph[x][i]);
else chain_partitioning(graph[x][i],graph[x][i]);
}
}
주석으로 설명해 두었으니 참고하시면 됩니다.
질의 함수 관련 코드는 아래 예시 문제를 통해 확인하겠습니다.
1을 루트로 하는 트리를 HLD하여 풀겠습니다.
검은색 돌의 dfs numbering이 작을수록, $1 \rightarrow v$로 가는 경로에서 1에 더 가깝습니다. (트리에서 dfs ordering하였으므로 자명합니다.)
세그 트리 또는 set 등을 이용하여 chain 정보와 최솟값을 관리해 주면 풀릴 것 같습니다.
시간복잡도는 $O(mlog(n))$에 가까운 $O(mlog^2(n))$인데, 세그트리로 나이브하게 $O(mlog^2(n))$ 짜면 시간초과가 발생합니다.
set으로 풀어보죠. 1번 쿼리가 들어올때마다 set에서 검은 돌의 정보를 관리하고, 2번 쿼리가 들어오면 $v \rightarrow 1$ 에서 만나는 sub chain의 정보를 모두 수집하여 vector에 저장합니다.
저장한 vector를 reverse해 주면 $1 \rightarrow v$이 됩니다. 코드를 보죠!
int query(int v){
if(black.empty()) return -1;
vector<pii> tmp;
while(grp[v]!=1){
tmp.push_back({num[grp[v]],num[v]});
v=par[grp[v]];
}
tmp.push_back({num[grp[v]],num[v]});
reverse(tmp.begin(),tmp.end());
for(auto xx:tmp){
int lft=xx.first, rgt=xx.second;
auto low=black.lower_bound(lft);
if(low!=black.end() && *low<=rgt) return rev[*low];
v=par[grp[v]];
}
return -1;
}
굳이 vector를 reverse해 주지 않아도 큰 문제는 없지만, set에 원소가 많을 경우 빠를 반환을 위해서 처리했습니다.
set이 아닌 segment tree와 연계되는 문제도 많으므로, 다양하게 풀어보시는 것을 추천드립니다 ㅎㅎ;;
